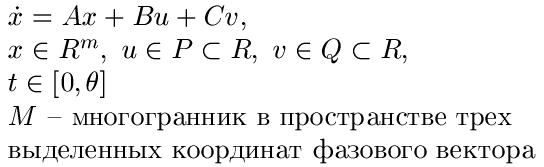
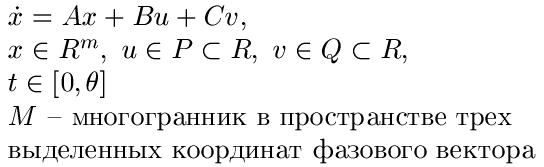
В исходной игре фазовый вектор x может иметь любую размерность
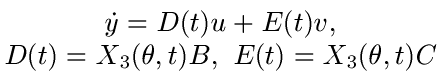
Стандартной заменой переменных (при помощи трех строк фундаментальной матрицы Коши) переходим к эквивалентной дифференциальной игре без фазовой переменной в правой части. Здесь фазовый вектор y имеет размерность 3.

Для построения максимального стабильного моста в рамках аппроксимирующей игры разбиваем ось времени с шагом Δ влево от момента
окончания θ точками
Построение сечений производится в попятной процедуре: на первом шаге на основе целевого выпуклого многогранника строится выпуклый многогранник
Построение очередного сечения
Для непрерывной, положительно однородной, кусочно-линейной функции γ :
При построении опорной функции
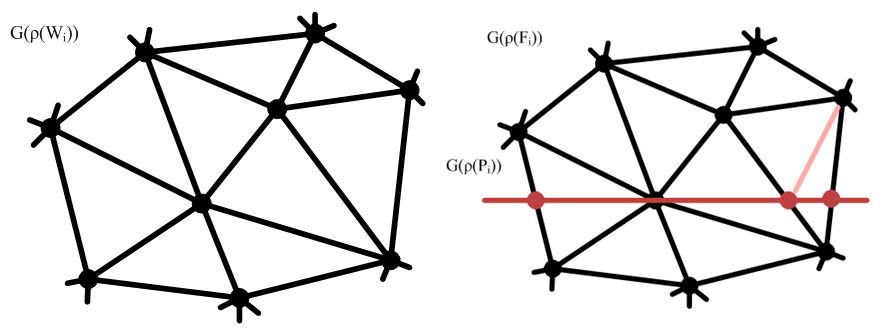
Сетка
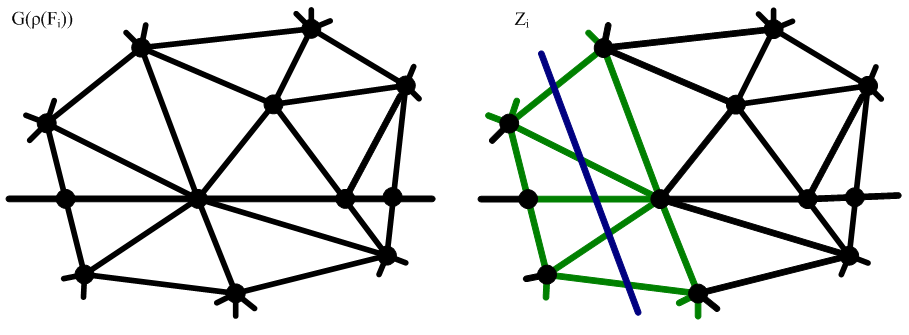
Пересчитываем значения опорной функции
Для перехода к опорной функции многогранника
С этой целью разработана итерационная процедура. Организуем список "подозрительных" связей между узлами.
Первоначально в этот список заносятся связи сетки
При разработке алгоритма построения максимального стабильного моста использованы идеи из указанных статей.
/* Подготовительные действия */ Получение структуры выпуклого многогранникаM=W0 по заданным вершинам Построение графа (сеткиG(ρ(W0)) ) выпуклого многогранника по его структуре Триангуляция построенного графа (сеткиG(ρ(W0)) ) /* Построение t-сеченийWi=W(ti) максимального стабильного моста W */ Цикл пока((θ-ti) < τf) { Построение сеткиG(ρ(Fi)) Построение набора П (набора связей, на которых функцияφi может быть не выпукла) Цикл пока набор П не пуст { Если функцииφi выпукла на первой связи из набора П, то { Удаляем первую связь из набора П } иначе { Корректировка функцииφi и набора П } } }
Приведенная схема алгоритма построения моста базируется на пошаговой процедуре нахождения t-сечений.
Итерационная процедура овыпукления является наиболее затратной при вычислении очередного сечения.
Поскольку представление действительных чисел на компьютере имеет ограниченную точность, возникают проблемы,
связанные с работой с близкими узлами и узкими треугольниками, возникающими вследствие малости углов между соседними связями.
Первая проблема преодолевается за счет “умного” первого игрока, который не создает очень близких узлов.
Второй вопрос решается за счет применения масштабирования вдоль направления наименьшей толщины многогранника.
Помимо этого, при построении очередного
t-сечения моста убираются все фиктивные грани, возникающие из-за того, что мы всегда работаем с триангулированной сеткой.
Представленная здесь программа позволяет просматривать уже просчитанные максимальные стабильные мосты. Для этого запустите программу (файл LinearDiff3DGame.OpenGLVisualizer.exe), выберите в меню "Actions" пункт "Load" и в появившемся диалоговом окне выберите файл с посчитанным мостом (файл типа .dat).
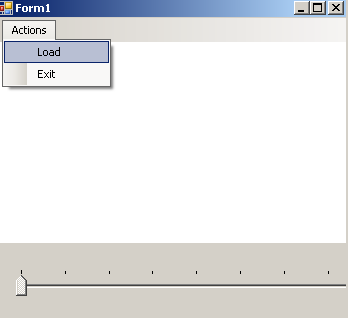
После того, как посчитанный мост загрузится, его можно просматривать, выбирая при помощи ползунка (внизу слева) просматриваемое
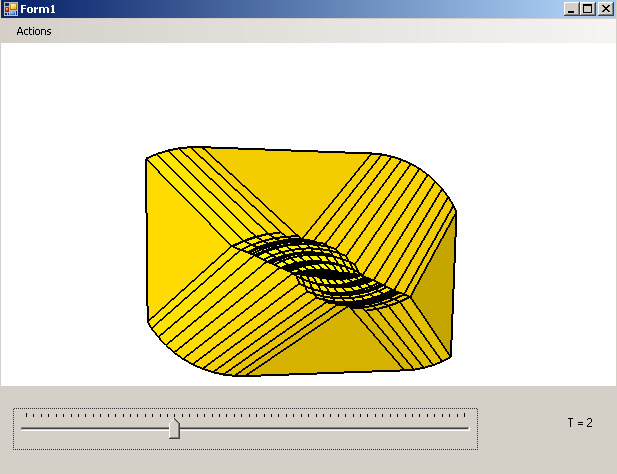
Архив с программой называется MaxStableBridgeBuilder.zip. Для работы программа требует операционную систему не ниже WindowsXP, предустановленный .NET Framework версии не ниже 3.5. При работе программы могут возникать артефакты визуализации, связанные с поддержкой OpenGL драйверами видеокарт.
Система имеет вид:
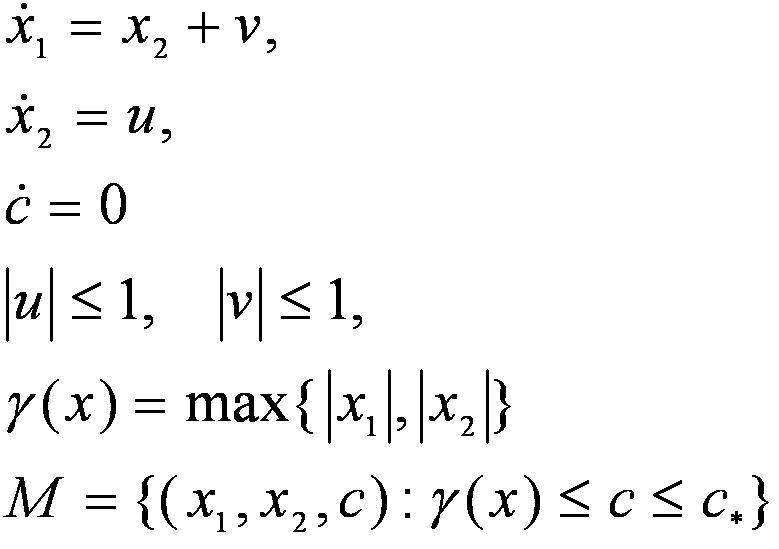
Параметры расчета моста: c* = 2.5, время окончания счета τf = 6. Посчитанный мост находится в файле MaterialPointBridge.dat. Каждое t-сечение представляет собой срезку на уровне c* надграфика функции цены дифференциальной игры с динамикой
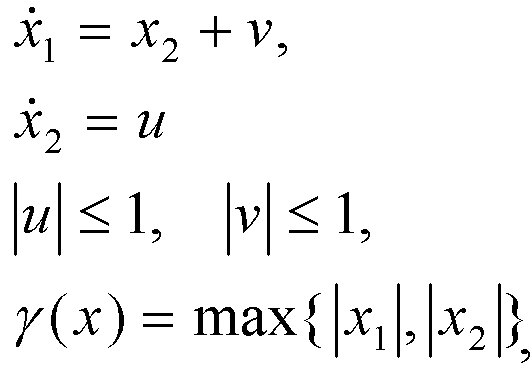
фиксированным моментом окончания и терминальной функцией платы γ.
Система имеет вид:
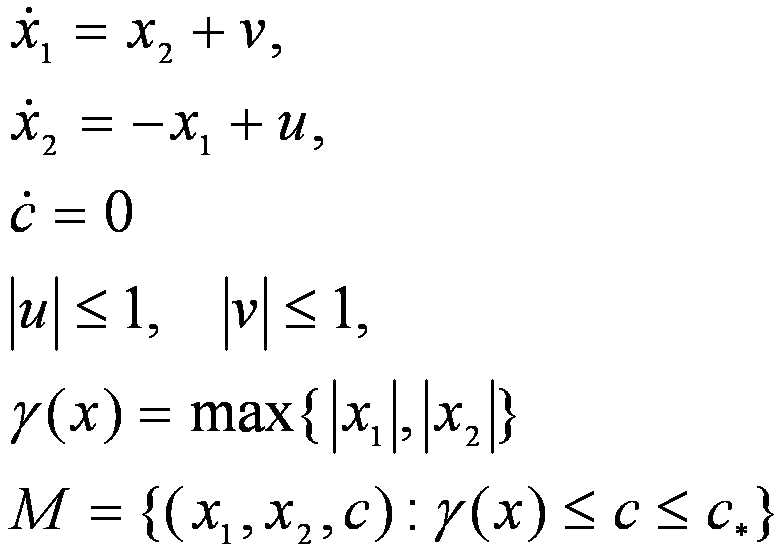
Параметры расчета моста: c* = 2.5, время окончания счета τf = 6. Посчитанный мост находится в файле OscillatorBridge.dat.
Система имеет вид:
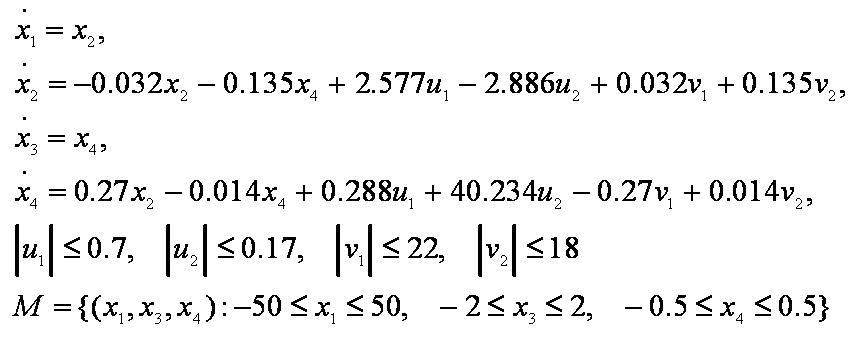
Параметры расчета моста: время окончания счета τf = 6. Посчитанный мост находится в файле AirplaneTaskBridge.dat.