Level Sets of the Value Function in Linear
Differential Games with Elliptical Vectograms
Download full text of the report (PDF format, 2375 KB)
Title

Our paper is a collection of four examples from
the differential game theory. We consider linear differential
games with fixed terminal time. For such games, a level set of
the value function is a tube in the game space "phase vector
× time".
If a game is regular, then every level set tube is smooth. Non-smoothness
and some other geometrical features of the tubes can tell us
about difficulties of the solution of the game.
Physical Pursuit Problem
Slide 1

Let us imagine a problem where a rocket pursues
another one. At the beginning, their nominal velocities and
courses are such that a collision is forecasted. The velocities
are quite large (and the nominal relative velocity is very large
also). The pursuer and evader controls are not too strong to
change the trajectories sufficiently. They can only correct the
trajectories slightly. The pursuer minimizes the miss distance,
the evader maximizes it. It is reasonable to measure the miss
distance not as the shortest distance between the objects during
the homing process, but as the distance between projections of
the geometrical states of the objects at the instant of the
nominal collision into the plane orthogonal to the direction of
the nominal relative velocity. Let take axes in this plane as
follows: the first axis is defined by the vectors of the nominal
velocities (that is the first axis is situated in the plane of
the nominal velocities vectors), and the second one is orthogonal
to it.
We consider the game from the point of view of
the first player (the pursuer). So, one can take into account the
inertia of the servo-mechanisms of the pursuer in the statement
of the problem. About the second player (the evader) it is
supposed that its control signals are realized instantly.
It is natural to linearize the dynamics of the
objects along the nominal motions.
Thus, we have a linear differential game with
fixed terminal time.
Formalization of the Pursuit Problem
Slide 2

An investigation of such linearized problem was
made in the works of J.Shinar and his collaborators. In the
Figure, the nominal motions and the forecasted collision point
are shown. It is supposed that the accelerations of both vehicles
are bounded and orthogonal to the respective nominal velocity
vectors. The corresponding dynamics vectograms are circular.
Dynamics of the Linear Model Game
Slide 3

We consider planar motions in the plane
orthogonal to the initial nominal relative velocity. When
projecting the original circular control constraints into this
plane, the new constraints become elliptical.
In the slide, the linearized dynamics is shown.
The phase vector is six-dimensional (two geometrical difference
coordinates, two difference velocities, two difference
accelerations). The constant kP
describes the inertia of servo-mechanisms of the pursuer. The
miss is computed as the distance from the origin to the
difference geometrical state at the terminal time.
In the papers of J.Shinar and his collaborators,
the results of analytical investigations of this linear
differential game were presented. The relations describing the
level sets of the value function were obtained. It was
established that the value function is not differentiable.
Singular surfaces were analyzed. The system of singular surfaces
for this problem contains dispersal, equivocal and focal pieces.
All computations were made by means of the
equivalent coordinates of the dimension two. The transformation
from the original six-dimensional vector to the equivalent one is
provided by the standard variable change which involves the
fundamental Cauchy matrix for the system dz/dt = A(t)z
(without the controls). The game space is three-dimensional: two
equivalent coordinates and the time.
Dynamics of the Equivalent Game
Slide 4

After the transformation to the equivalent
coordinates, the dynamics of the game has the form shown in the
slide. The terminal instant and control constraints are the same
as in the original game. The payoff function is the norm of the
equivalent phase vector x
at the terminal instant.
Further, some results numerically obtained for
this game are presented. Standard programs for solving
differential games developed in the Institute of Mathematics and
Mechanics (Ekaterinburg, Russia) were used. Numerical data for
the example are shown in the slide.
Tubes of Vectograms
Slide 5
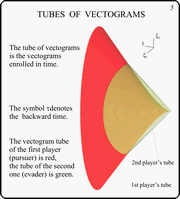
To understand the structure of level sets of
the value function, it is useful to consider tubes of players
vectograms. The tube of vectograms of the first player is the set
P(t)=X1,4(T,t)BP
enrolled in time. In the same way, the tube of vectograms of the
second player is understood.
In the Figure, the first player's tube of
vectograms is shown by red color, and the second player's one is
green. The latter is made transparent. Contours of some t-sections
are drawn on it. The symbol t denotes the backward time.
In this example, the second player's tube of
vectograms is an elliptical cone. The first player's tube also
has elliptical t-sections which grow non-linearly. For
small values of the backward time t, the second player
has full advantage: t-sections of his tube include
corresponding t-sections of the tube of the second
player. After some instant, the first player gets advantage in
vertical direction and in directions close to the vertical one.
With increasing the backward time, the first player takes the
full advantage.
General View of the Critical Tube
Slide 6
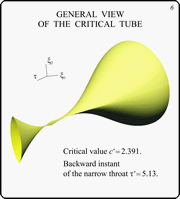
In this slide, a level set of the value function
is shown. It corresponds to a value c* of the payoff
function. This level set is infinite in time. It has a narrow
throat. After the throat, the level set enlarges with growing the
backward time.
The considered value c* is the critical one: for less
values of c, corresponding level sets are finite in time.
With small decreasing of the parameter c, level set
breaks near the throat.
In the picture, the changing of t-section orientation
can be seen: before the throat they are oriented horizontally,
after the throat they become oriented vertically. Namely, these
facts give difficulties to the solution of the considered
differential game. In this situation, the numerical results show
adequately the structure of level sets near the throat and
correspond well to the analytical results only if very precise
computations are used.
Large View of the Narrow Throat
Slide 7
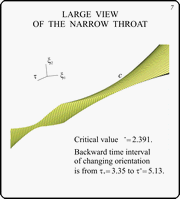
This slide contains a zoomed view of the narrow
throat. Contours of some t-sections are shown.
The Critical Tube And Close Ones
Slides 8, 9
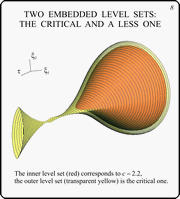
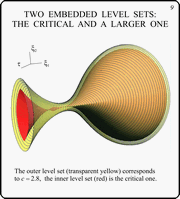
These two slides show the critical level set with
close ones. The slide 8 contains the critical level set (yellow
transparent) and a set corresponding to a bit less value of the
parameter c (red). The slide 9 demonstrates the critical
level set (red) with a set corresponding to a bit greater value
of the parameter c (yellow transparent).
In the theory of differential games, there is a
well-known example "the boy and the crocodile". This
game has also a narrow throat for critical tube. But t-sections
are circular in the game "the boy and the crocodile".
The J.Shinar's example is more complicated.
The following question is very natural: how typical is the
situation of presence of throats, and how many throats can a
level set have?
With this object in mind, the authors have turned to the class of
differential games known in Russian literature on differential
games as the "L.S.Pontryagin's generalized test example".
Generalized L.S.Pontryagin's Test Example
Slide 10

The slide shows the dynamics of the L.S.Pontryagin's
generalized test example. The case is considered when the objects
move in a plane, that is the x and y are two-dimensional
vectors. The terminal time of the game is fixed. The payoff
function is defined as the geometrical distance between the
objects at the terminal instant. The first player minimizes the
payoff function, the second one maximizes it.
The Generalized Test Example is
Check One for Many Theoretical Works
Slide 11

Here is a list of authors who investigated the L.S.Pontryagin's
generalized test example or used it as a check one for new
theoretical methods. Very often, the time of termination is not
fixed. The game with fixed terminal time appears in this case as
a basis for the solution.
As a rule, the constraints P and Q were taken
circular. We consider the case when the constraints P
and Q are ellipses.
Model Example of J.Shinar as
Generalized Test Example
Slide 12

In the model example investigated by J.Shinar, the
evader governs a material point with inertialess control, and the
pursuer has inertial control circuit. The dynamics can be
rewritten as it is shown at the bottom of the slide. So, this
problem is a particular case of the L.S.Pontryagin's test example.
Change of Variables.
The Game in the Standard Form
Slide 13

With introducing new variables, the dynamics of
the test example can be presented in the standard form.
Transformation to the Equivalent Coordinates
Slide 14

The payoff function depends only on two components
of the phase vector at the terminal instant. So, by means of the
well-known change of variables which involves two rows of the
fundamental Cauchy matrix, one can pass to the equivalent game.
The phase vector of the equivalent game is two-dimensional.
Three following slides describe shortly the
idea of the backward computational procedure for constructing a
collection of t-sections of a level set of the value
function.
Scetch of a Level Set
Slide 15
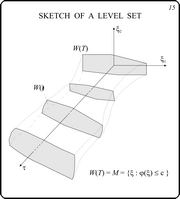
This slide explains the scheme of the backward
procedure. The algorithm starts with the payoff function level
set (Lebesgue set) corresponding to a number c. Then a
collection of t-sections of the value function level set
is constructed for a given time grid. This level set corresponds
to the chosen number c. In general, this is the method
of dynamical programming in application to differential games.
Approximating Game
Slide 16

For numerical procedure, some approximations are
made. The dynamics of the equivalent games is changed by a
piecewise-constant one. The constraints P and Q
are substituted by convex polygons. The payoff function j is
approximated by a function which has convex polygonal level sets.
Procedure of Convex Hull Construction
Slide 17

The transformation from one section to the next
one is provided by a specialized procedure. In its basis, it has
an algorithm for constructing convex hull of a positively
homogenious piecewise-linear function. The formula for
computation of this function is shown in the slide. Here, D is the step of the
time grid.
Further, three example of differential games
are presented. Some their level sets have narrow throats. It was
not too easy to find these examples. But authors are sure that
the presence of such throats is quite typical.
Exampe 1
Slide 18

The dynamics of the first example is written in
this slide. The first player governs an inertial point in the
plane. The second object is a two-dimensional mathematical
pendulum. Both objects have friction proportional to the velocity.
The constraints on the player controls are taken as ellipses.
Example 1. The Players' Vectogram Tubes
Slide 19
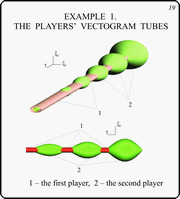
In this slide, two views of the tubes of
vectograms for both players are presented. The green tube belongs
to the first player, the red one is of the second.
Since the second player dynamics is oscillating,
the advantage changes in time. At the beginning of the backward
time, the second player has full advantage, but for sufficiently
large values of the backward time t, the first player gets the
advantage.
Example 1. The Level Set With a Narrow Throat
Slide 20

This slide shows the level set for c =
2.451. One can see the varying orientation of t-sections
of the set. At the beginning, they are have vertically elongated
orientation. Further, t-sections become horizontally
elongated. This change is determined by delicate interaction of
the vectograms.
This example was computed in the interval t Î [0,20]. The time
step D
= 0.05. The level set of the payoff function j was 100-gon.
The ellipses P and Q were approximated by
polygons with 100 vertices.
The Large View of the Narraw Throat
Slide 21

In this picture, a zoomed view of the tube is
drawn. It can be seen that the level set degenerates almost to a
point.
Example 2
Slide 22

Here, the second example is presented. In this
case, both players govern oscillating objects. It is noticeable
that the constraints on the player controls are taken as
coinciding ellipses.
Despite the ellipses of the constraints
coincide, the computations are not trivial, because there is no
uniformity of the players vectograms and level sets of the payoff
function.
Example 2. The Players' Vectogram Tubes
Slides 23,24

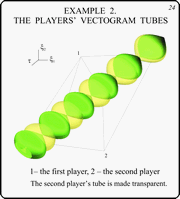
These slides demonstrate the tubes of vectograms
for the second example. The green tube belongs to the first
player, the yellow one is of the second. In the 24th slide, the
latter is transparent.
Example 2. The Level Set With Two Narrow
Throats
Slide 25
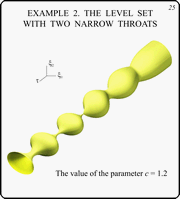
This slide gives the general view of the level set
for c = 1.2. This level set has two narrow throats. They
correspond to the instants t1 = 5.65 and t2 = 8.50.
This example was computed in the interval t Î [0,20]. The time
step D
= 0.05. Near the throats, 10 times less step was used: D = 0.005. The level
set of the payoff function j was approximated by a regular 100-gon.
The ellipses P and Q were approximated by
polygons with 100 vertices.
Example 3
Slide 26

Here, the dynamics of the third example is shown.
Again, two oscillators with elliptical constraints.
Example 3. The Players' Vectogram Tubes
Slide 27
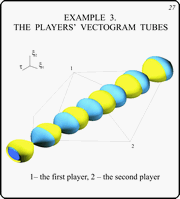
In this figure, the tubes of the players
vectograms are drawn.
Example 3. The Level Set With Three Narrow
Throats
Slide 28
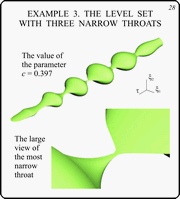
In this slide, the level set having three narrow
throats is demonstrated. The level set corresponds to c
= 0.397.
Example 3. The Level Set and the Vectogram
Tubes
Slide 29
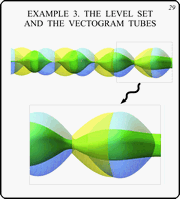
Here, the tubes of vectograms are put on the level
set. All colors correspond to ones used before: the blue tube is
the tube of the first player vectograms, the yellow tube is of
the second player vectograms, and the green one is the level set.
The tubes of vectograms are transparent.
Variation of the level set in time is clearly connected to the
character of this or that player advantage. When the second
player has full advantage (when the yellow tube contains the blue
one completely), the level set contracts. Vice versa, when the
first player gets full advantage, the level set enlarges. If no
player has full advantage (that is both players have partial
advantage), the situation with the level set changing can be more
complicated: growth to some directions and decreasing to others
could take place.
All comments

The Whole Booklet (all slides and comments
in PDF)

S.S. Kumkov, V.S. Patsko
Institute of Mathematics & Mechanics Ural Branch of RAS
S.Kovalevskaya str.16
620219 Ekaterinburg, Russia
e-mail:
sskumk@gmail.com
patsko@imm.uran.ru
J.Shinar
Faculty of Aerospace Engineering, Technion - Israel Institution of Technology,
Haifa, 32000, Israel,
e-mail:
aer4301@aerodyne.technion.ac.il






























