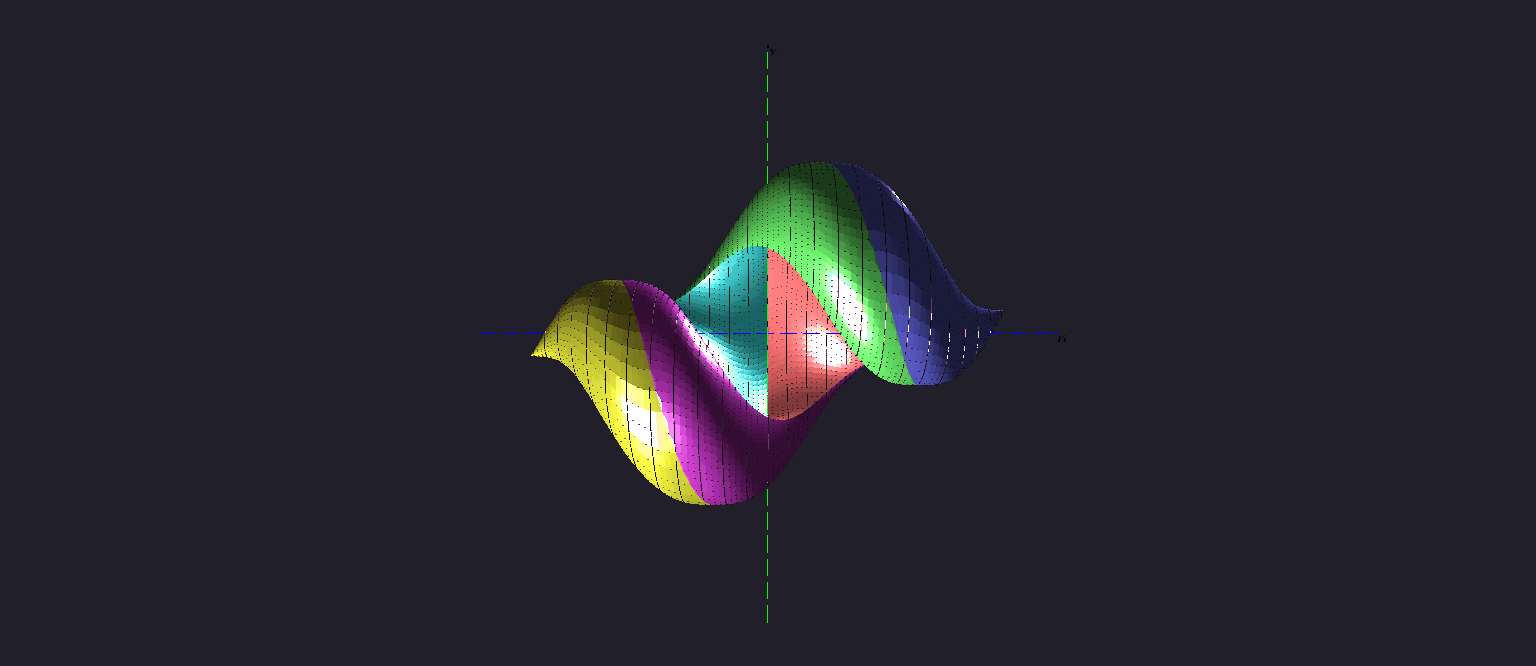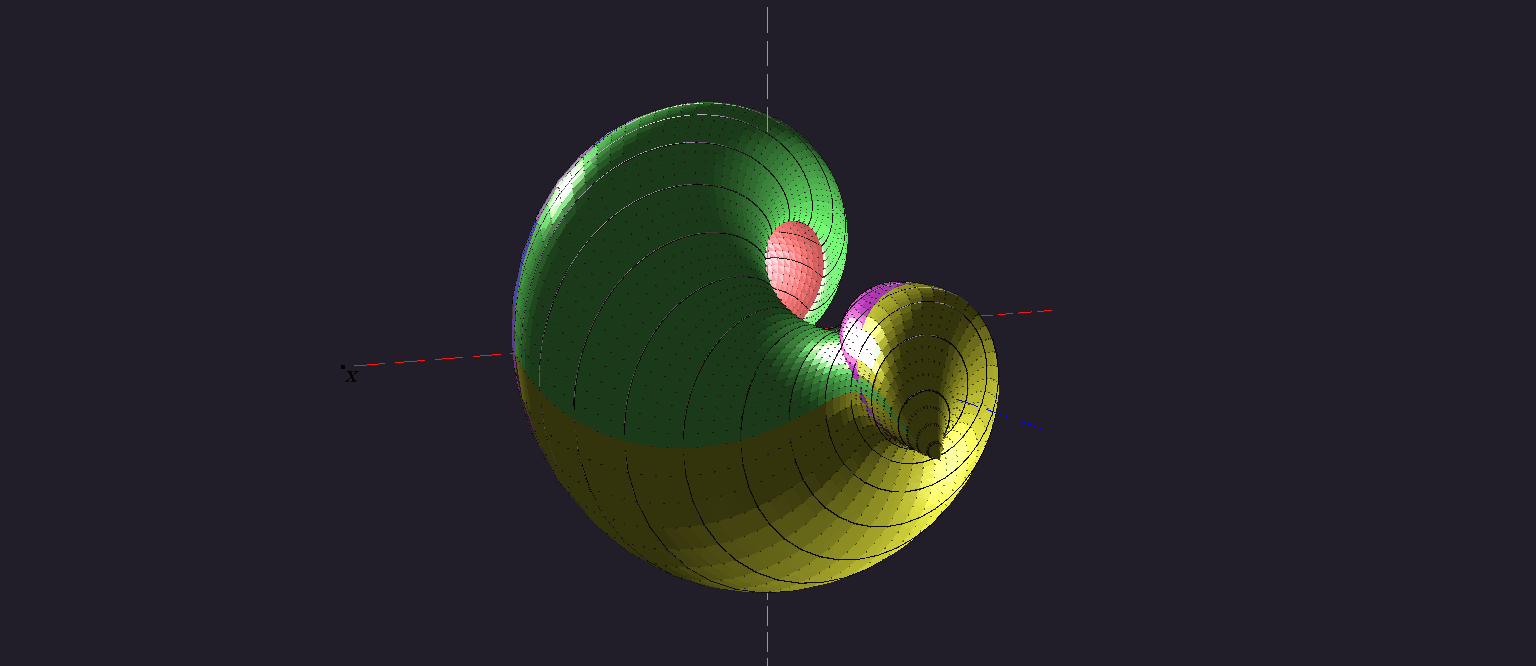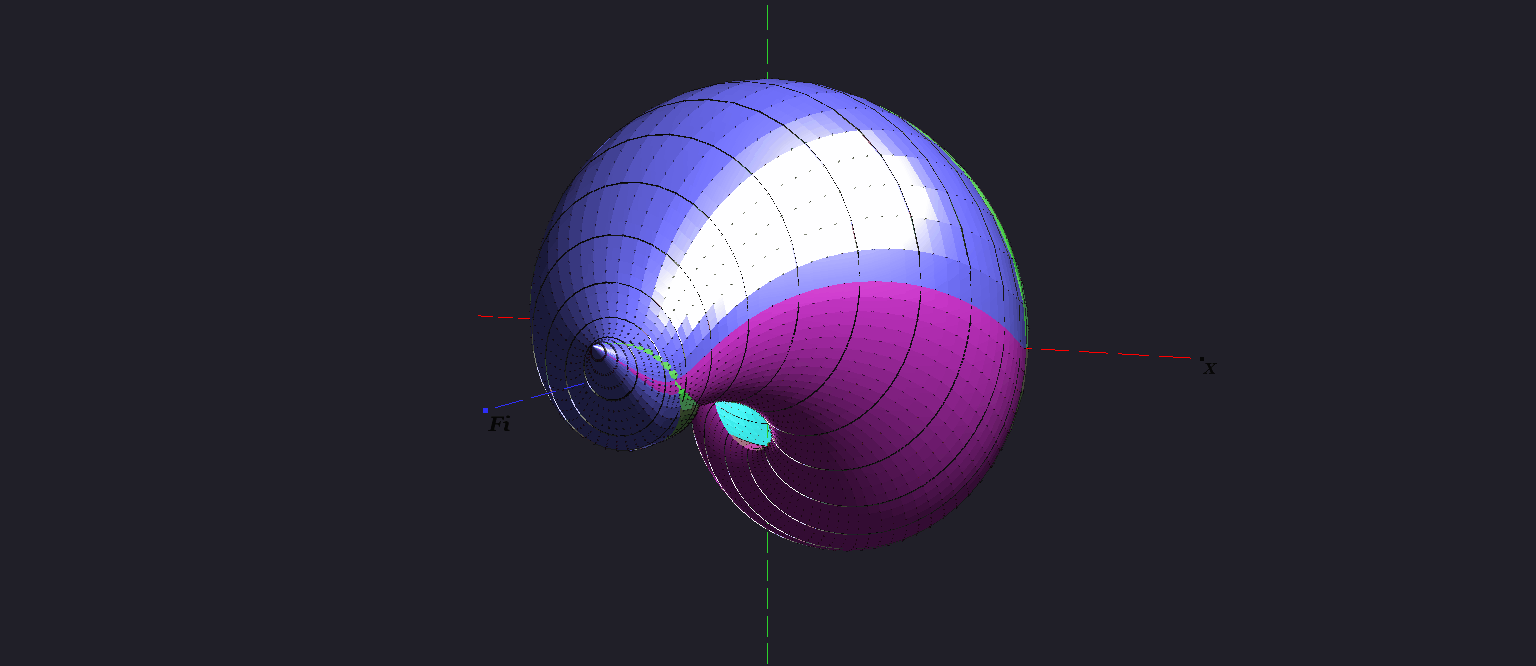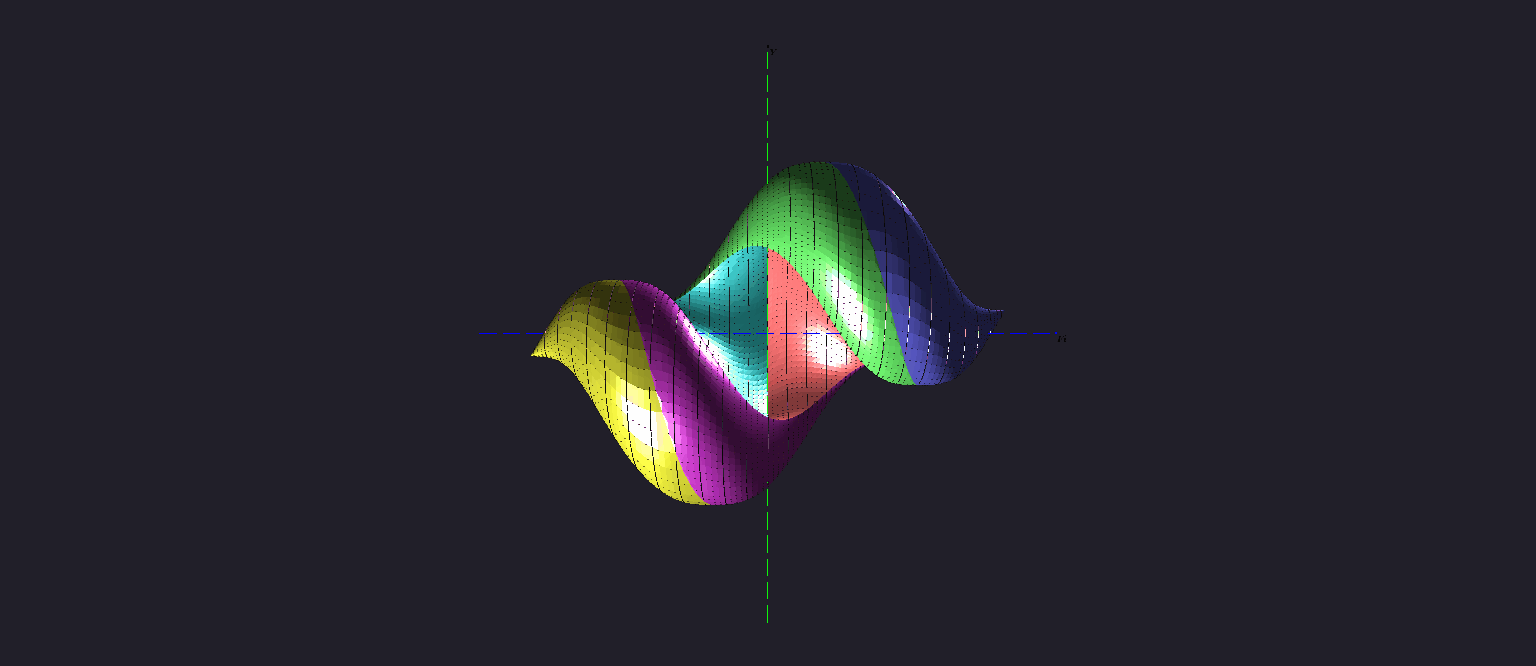
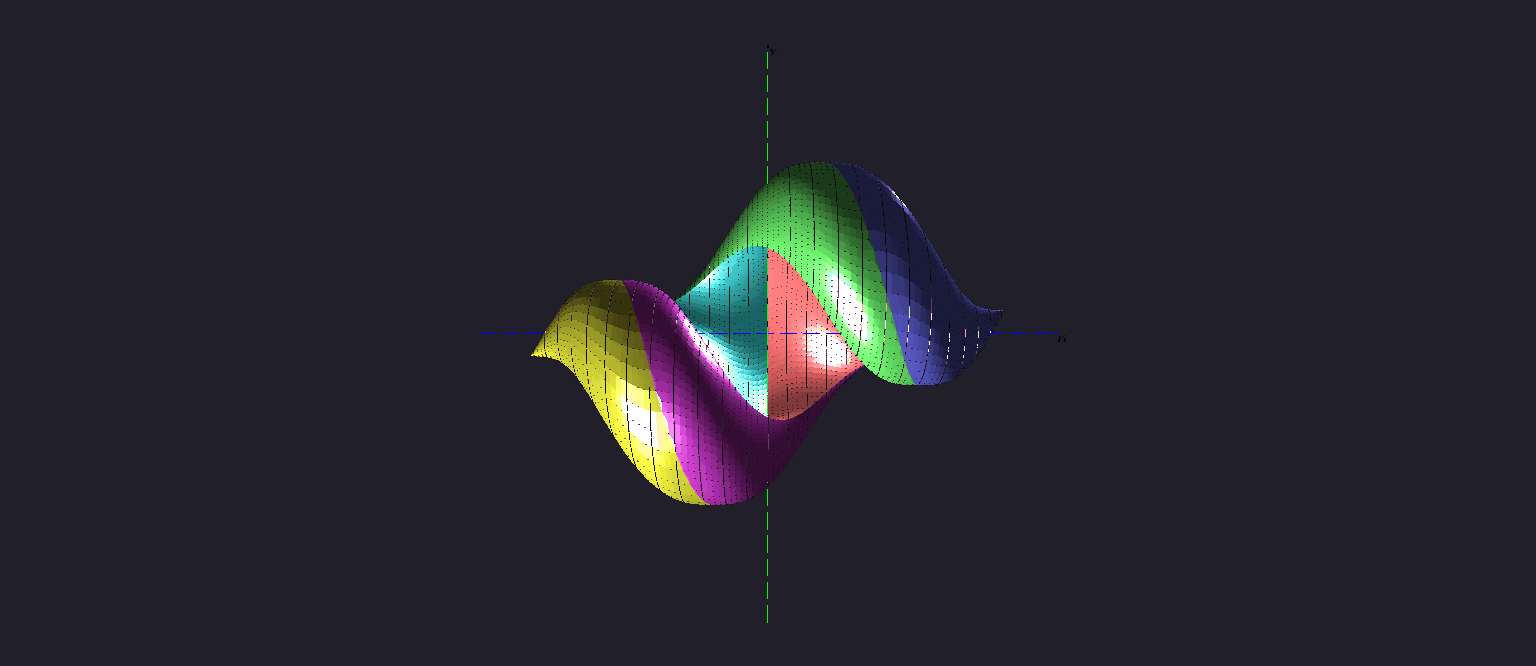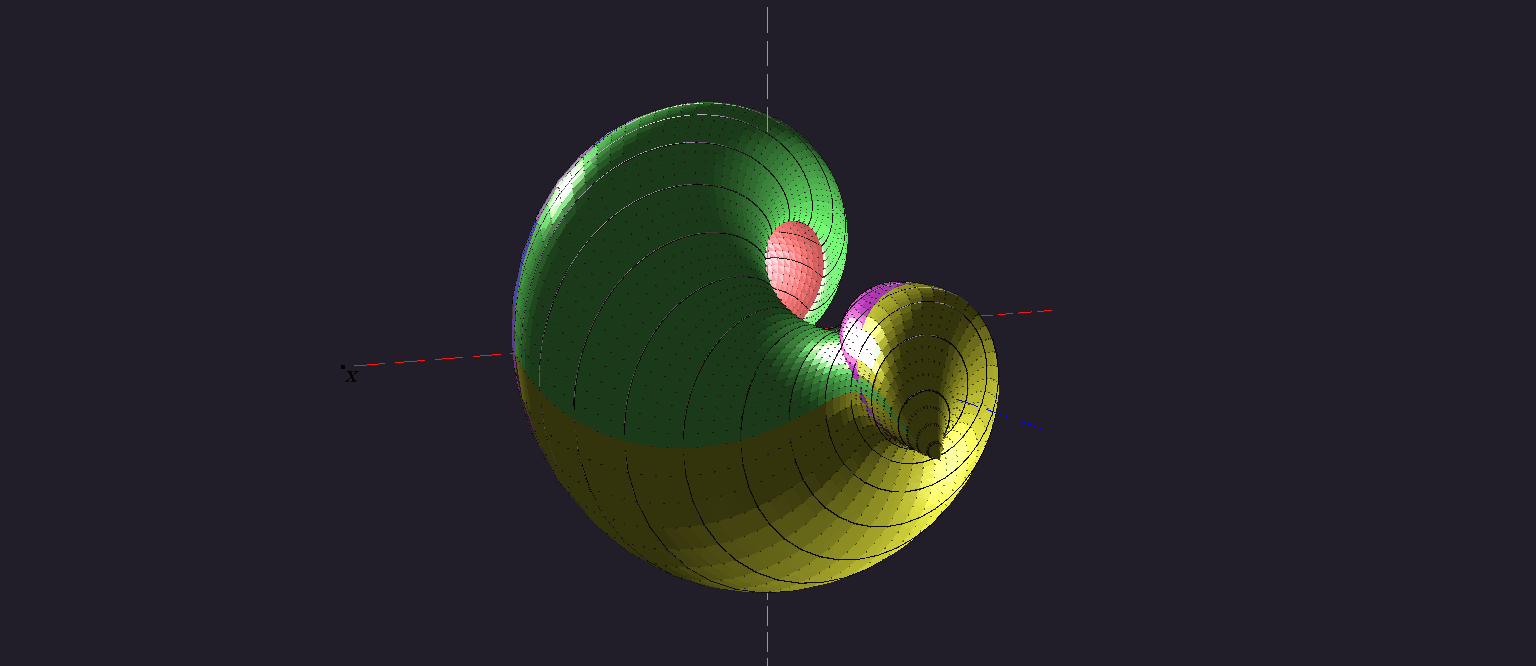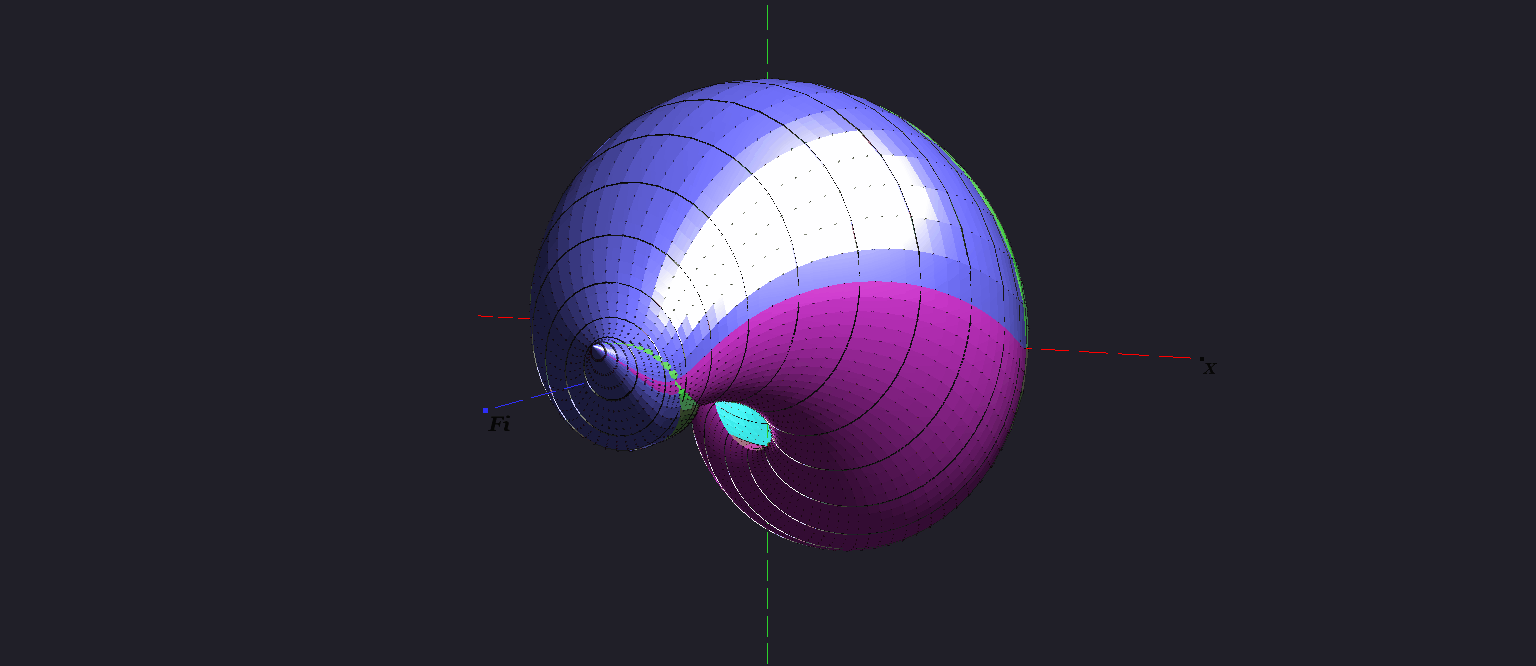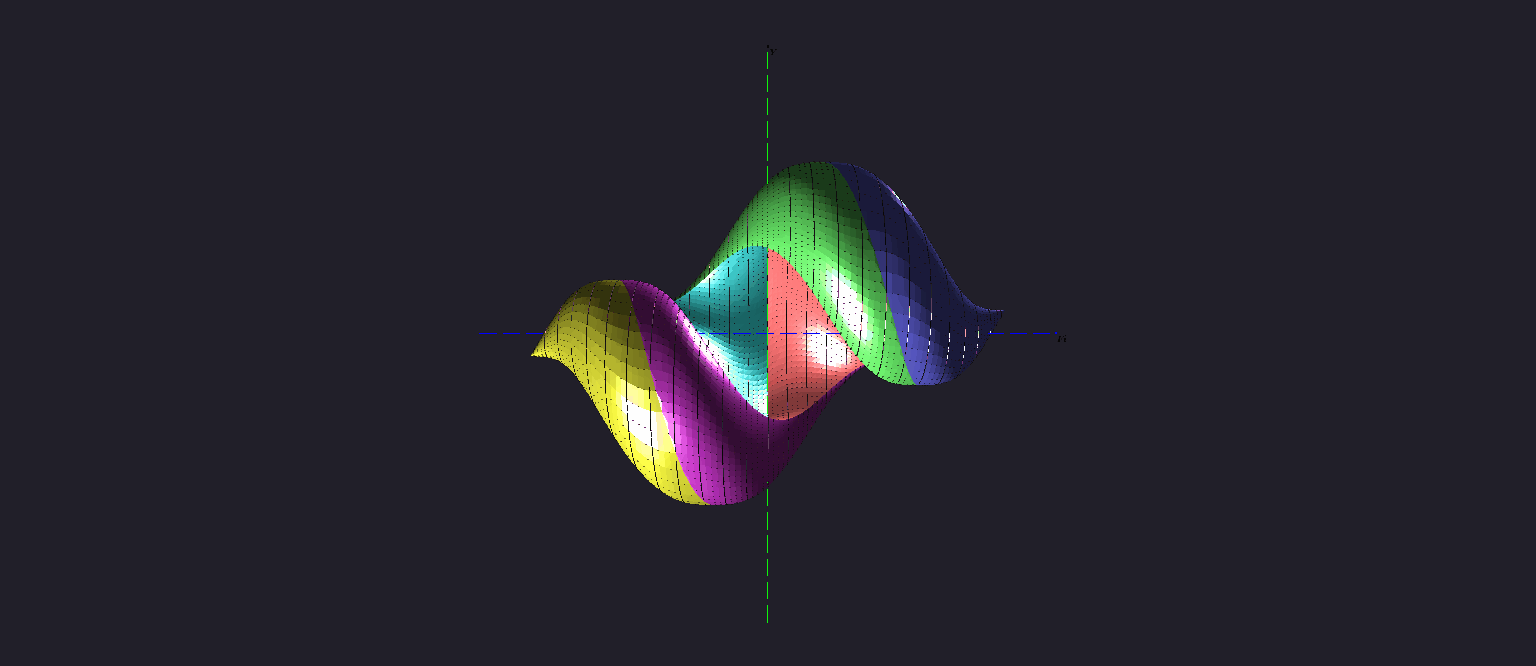
There is a video showing the three-dimensional reachable set "at the instant" tf = 2.5 π for the canonical Dubins' car. At this instant, the reachable set has not "wrapped up" completely yet.
There is a video showing the motion (a yellow ball) going from the initial zero point to a specially selected point on the boundary of the three-dimensional reachable set at the instant tf = 3.1 π for the canonical Dubins' car.
If the video doesn't play, download it
A part of the trajectory is shown in the time interval from 0.1 π to 3.1 π. At any instant from this interval, the point of the considered motion is on the boundary of the reachable set.
At the instant tf = 3.1 π, the three-dimensional reachable set is simply connected, but some of its two-dimensional cross-sections by the angular coordinate are not simply connected.
At the instant tf = 3.1 π, the trajectory is located at a point with the angular coordinate 0.9 π. This point coincides with the point to which the inner "hole" in the corresponding two-dimensional section is "collapsed". Such a point is located strictly inside of the specified cross-section. Nevertheless, this point lies on the boundary of the three-dimensional reachable set at this instant.
If the video doesn't play, download it
There is a video showing a motion bundle emerging from the initial zero point of the three-dimensional phase space. All the motions arrive at some given point on the boundary of the reachable set at the instant 4 π. The trajectories are shown in the time interval from 1 π to 4 π. Until the instant 1.5 π, all motions coincide.
At the instant 1.5 π, splitting into several trajectories begins (a total of 6). The splitting ends at the instant 2 π. In the interval from 2 π to 3.5 π, there are six motions. Then, in the time interval from 3.5 π to 4 π, the motions are joined back into one motion.
Thus, here we have a bundle of motions going from the starting point to the end point. Each motion follows the boundary of the reachable set.
The visualization material is prepared using a visualization package developed by Pavel A. Vasev (Laboratory of computer graphics, IMM UB RAS).
Vasev P.A., Patsko V.S., Fedotov A.A. Three-dimensional reachable set for the Dubins car, animation materials // III International Seminar dedicated to the 75th anniversary of Academician A.I. Subbotin "Control Theory and Theory of Generalized Solutions of Hamilton–Jacobi Equations". Ekaterinburg, Russia, 26–30 October, 2020.
Valerii Patsko and staff homepage
Страничка Сектора 3 (В.С.Пацко) Отдела динамических систем Института математики и механики Уральского отделения РАН.