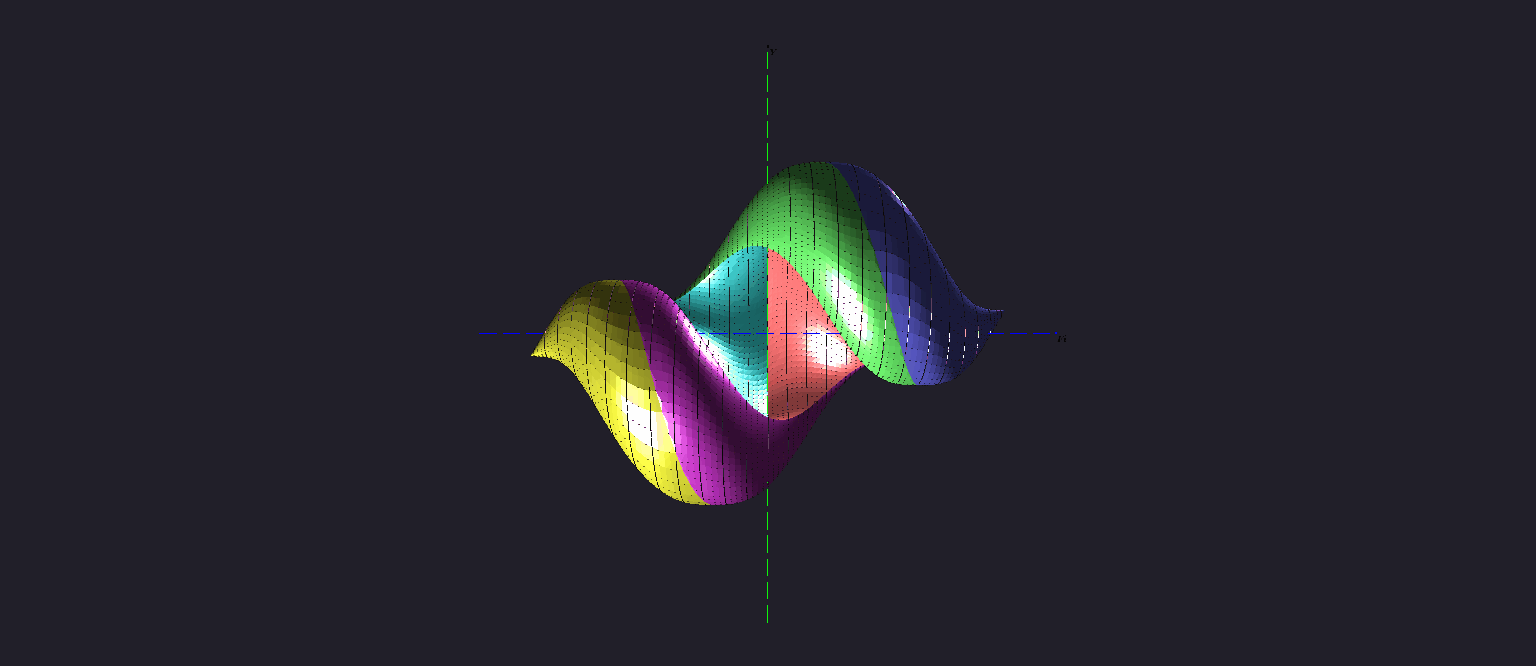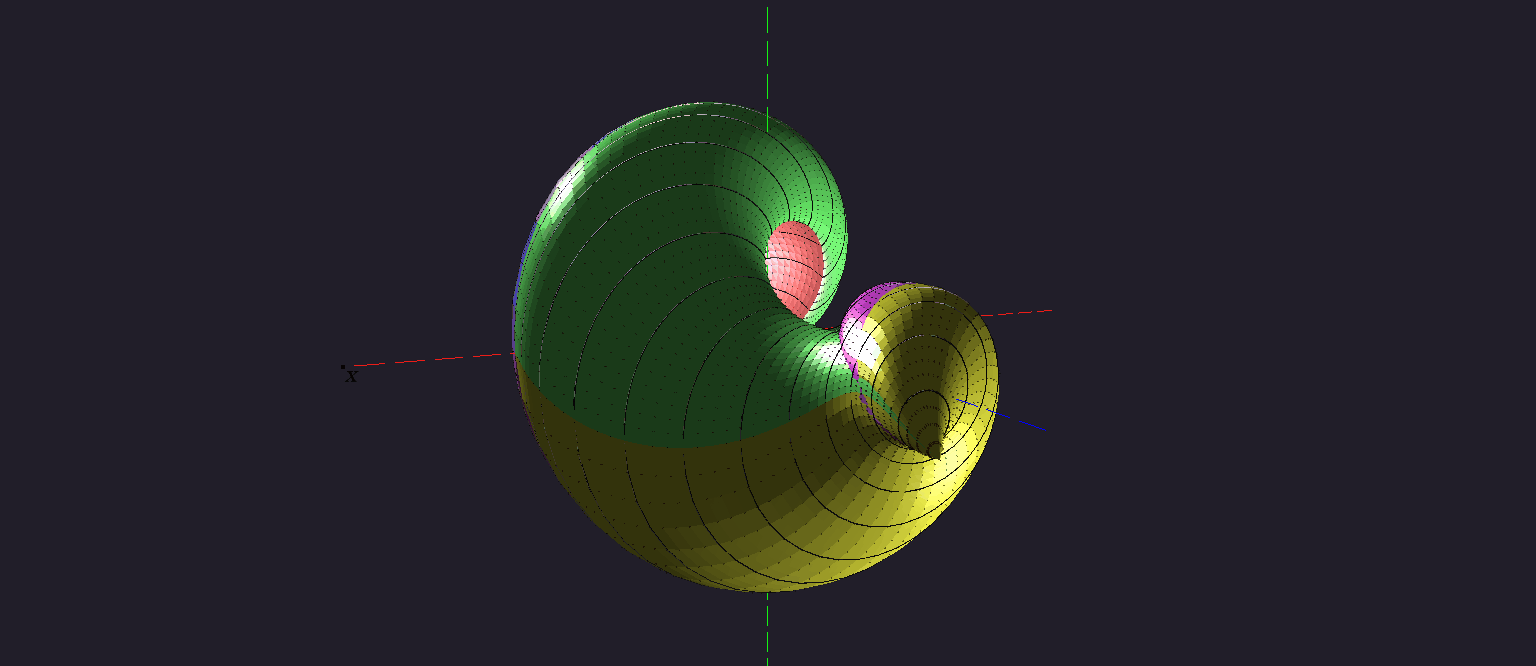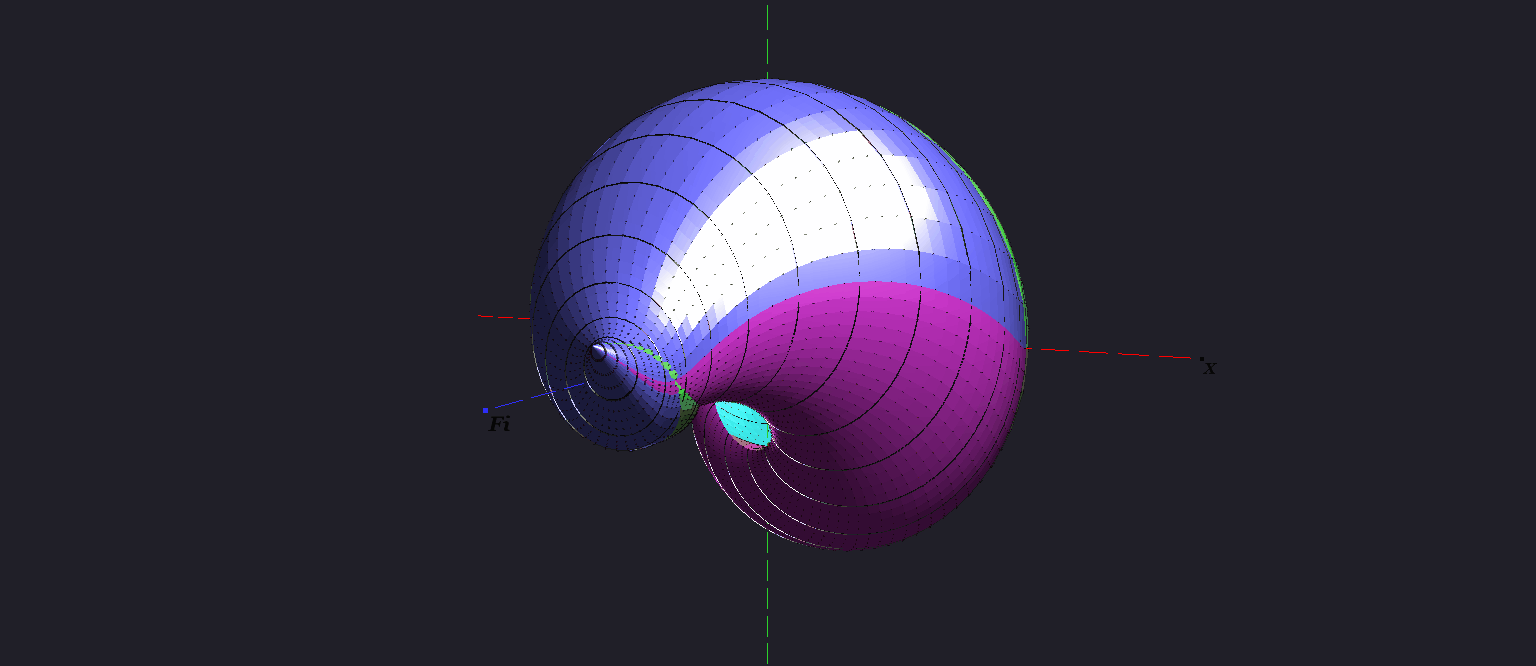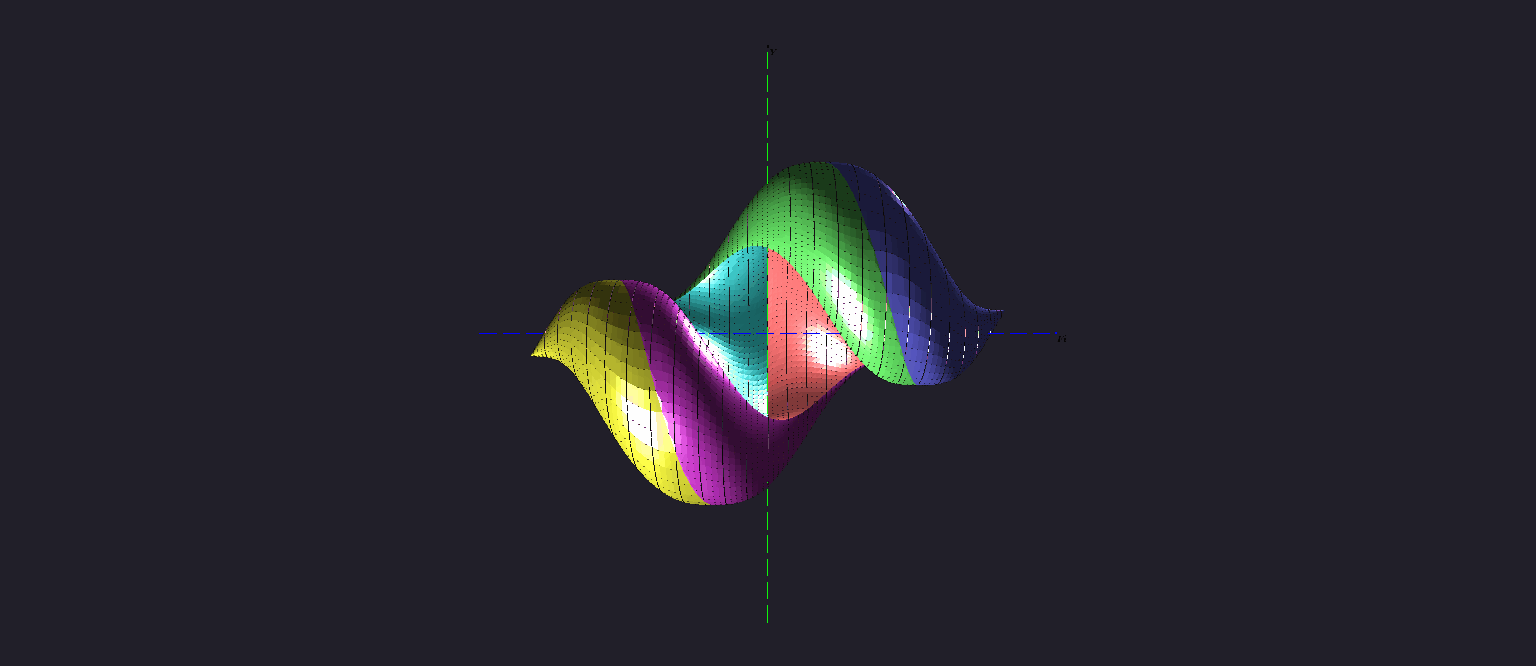
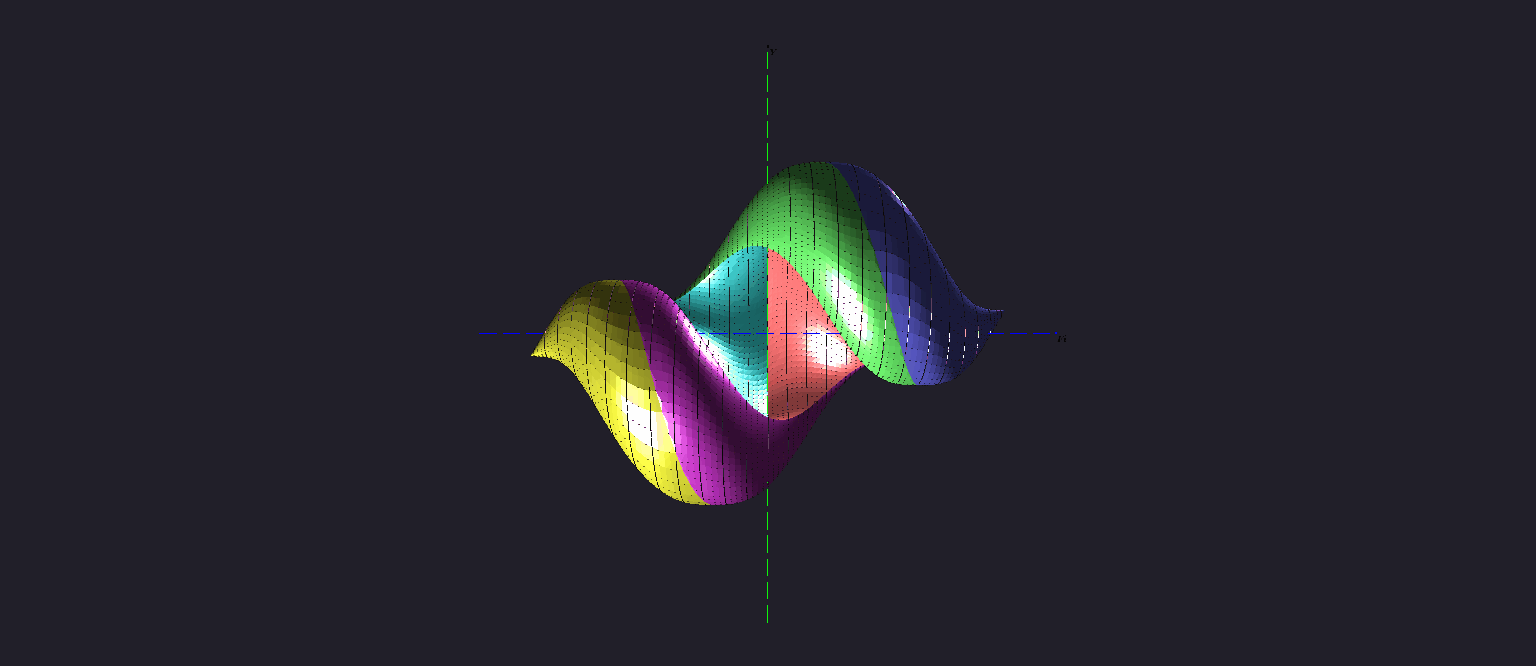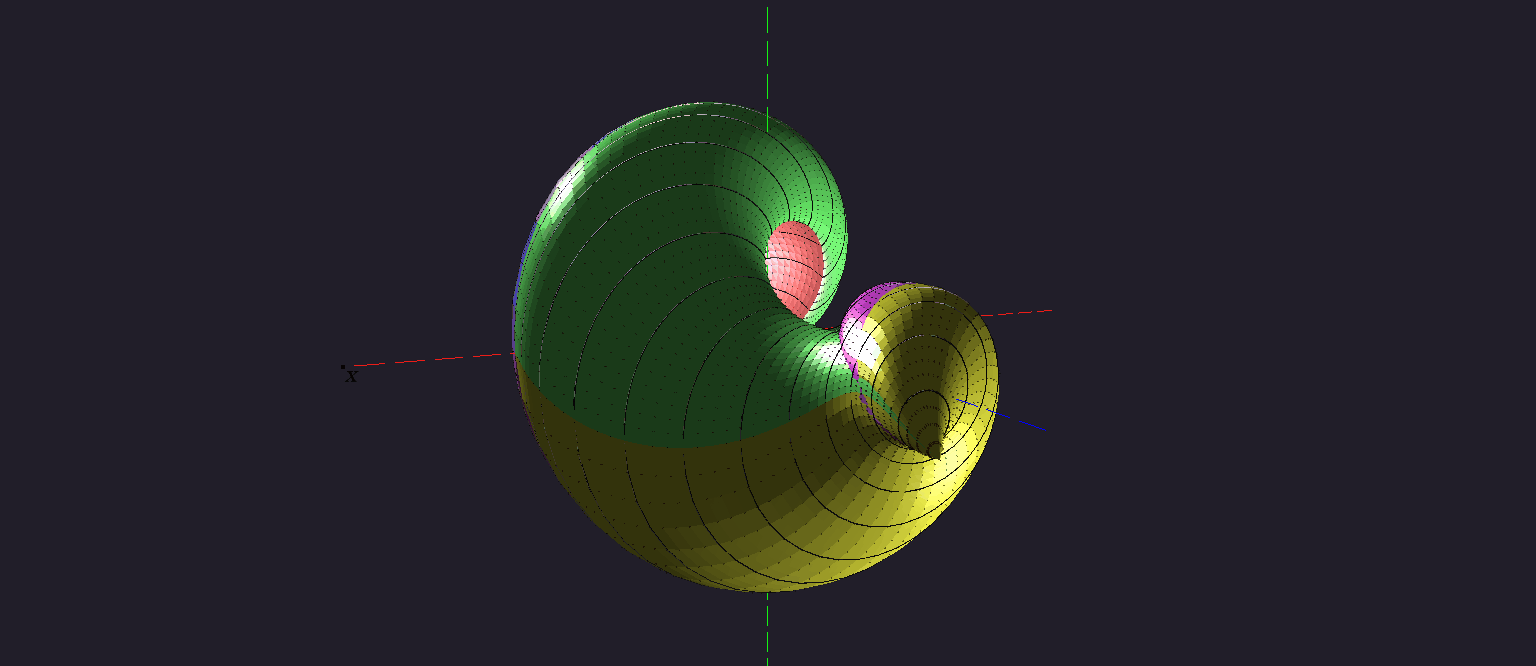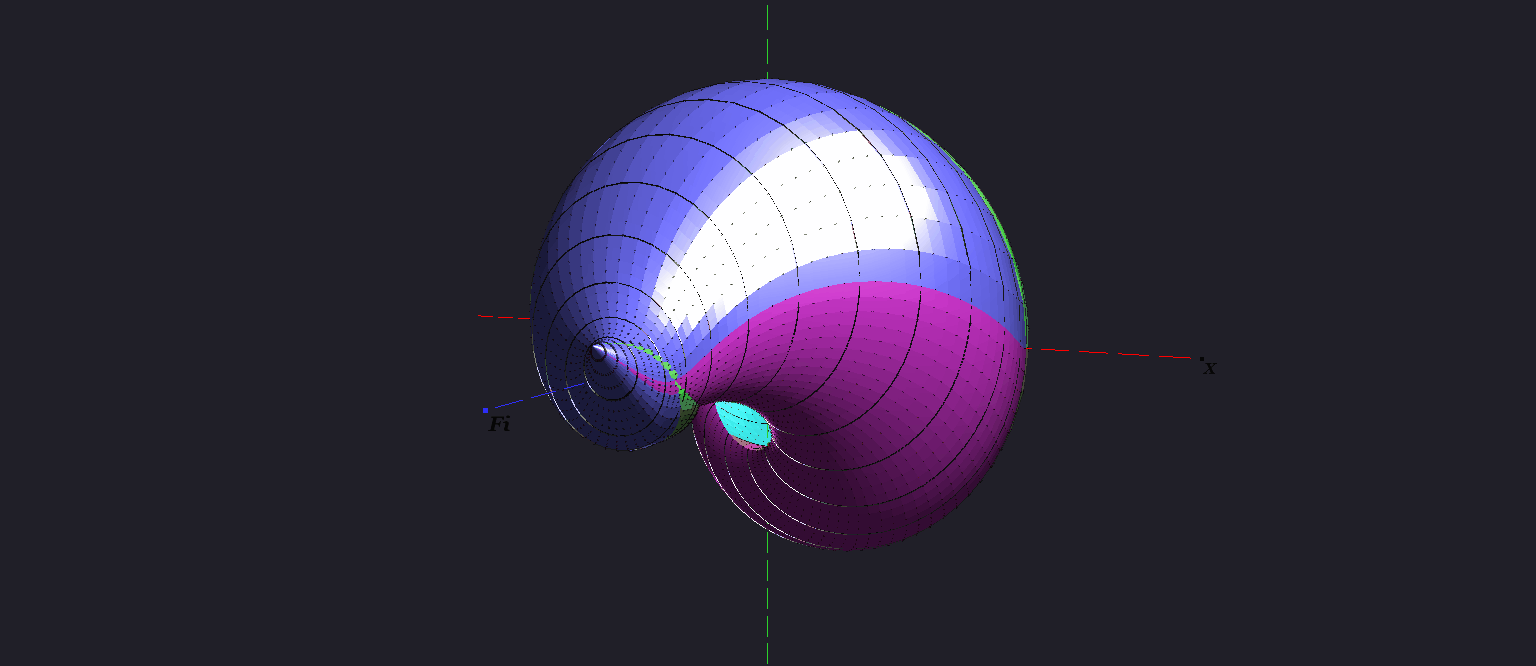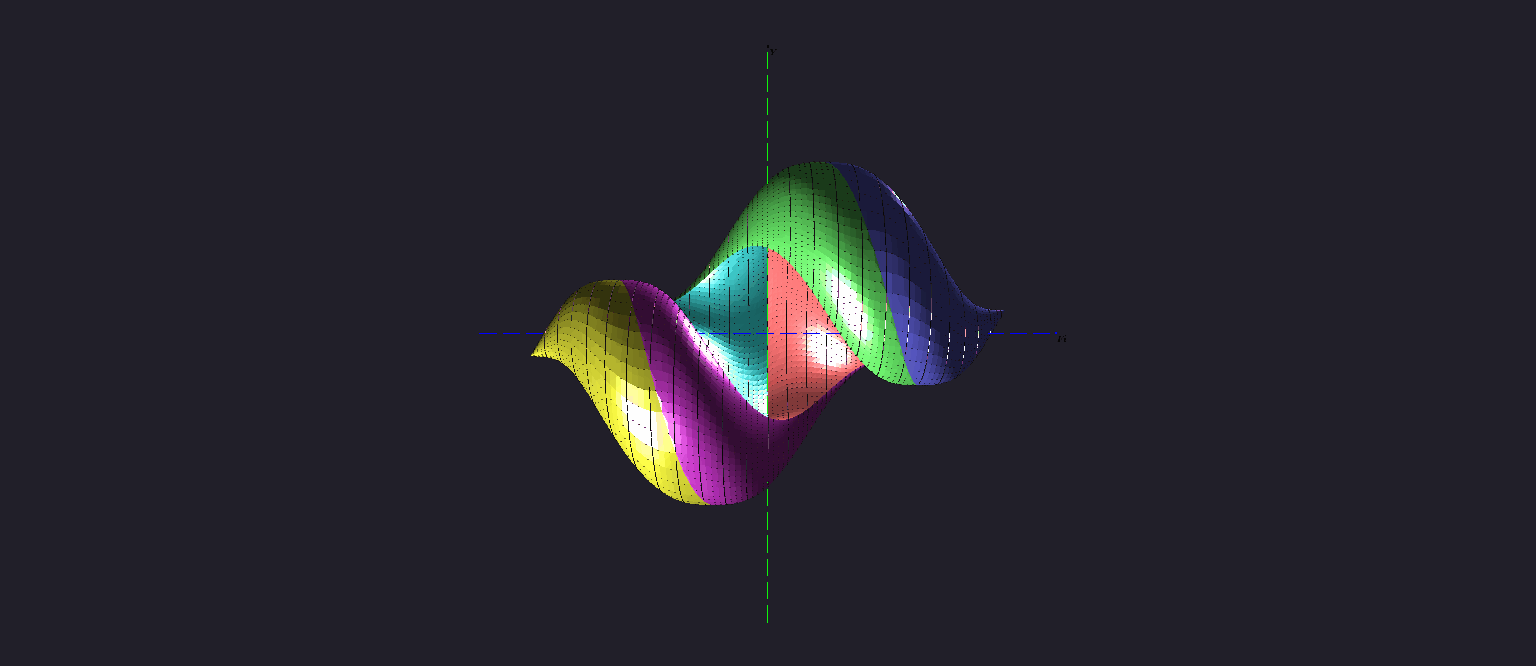
Представлена анимация, в которой показывается с разных ракурсов трeхмерное множество достижимости "в момент" tf = 2.5 π для канонической машины Дубинса. В этот момент множество достижимости ещe полностью не "завернулось".
Анимация с показом движения (желтый шарик), идущего из начальной нулевой точки в специально подобранную точку на границе трехмерного множества достижимости в момент tf = 3.1 π для канонической машины Дубинса.
Если видео не воспроизводится, скачайте его
Показывается участок траектории на интервале времени от 0.1 π до 3.1 π. В любой момент из этого интервала точка рассматриваемого движения находится на границе множества достижимости.
В момент tf = 3.1 π трехмерное множество достижимости является односвязным, но часть его двумерных сечений по угловой координате уже односвязными не являются.
В момент tf = 3.1 π траектория находится в точке с угловой координатой 0.9 π. Данная точка совпадает с точкой, в которую "выродилась" внутренняя "дырка" в соответствующем двумерном сечении. Такая точка находится во внутренности указанного сечения. Тем не менее, данная точка лежит на границе трехмерного множества достижимости в этот момент.
Если видео не воспроизводится, скачайте его
Здесь расположено видео, показывающее пучок движений, выходящий из начальной нулевой точки (трехмерного фазового пространства). Все движения приходят в некоторую заданную точку на границе множества достижимости в момент 4 π. Траектории показываются на промежутке времени от 1 π до 4 π. До момента 1.5 π все движения совпадают.
В момент 1.5 π начинается расщепление на несколько траекторий (показано 6 штук). Расщепление заканчивается в момент 2 π. На промежутке от 2 π до 3.5 π идут шесть движений. Далее на промежутке времени от 3.5 π до 4 π движения соединяются в одно движение.
Таким образом, здесь мы имеем пучок движений, идущих из начальной точки в конечную. Каждое движение идет по границе множества достижимости.
Материал подготовлен с помощью пакета визуализации, разработанного Павлом Александровичем Васевым (Сектор компьютерной визуализации, ИММ УрО РАН).
Васёв П.А., Пацко В.С., Федотов А.А. Трехмерное множество достижимости для машины Дубинса, анимационные материалы // III Международный семинар "Теория управления и теория обобщенных решений уравнений Гамильтона – Якоби", посвященный 75-летию со дня рождения академика А.И. Субботина. г. Екатеринбург, 26–30 октября 2020 г.
На страницу сектора В.С. Пацко
Страничка Сектора 3 (В.С.Пацко) Отдела динамических систем Института математики и механики Уральского отделения РАН.