

The talk is devoted to reachable sets for two very simple models of the car's dynamics. We call them ''mathematical cars''.
The simplest model is to the left. The name "Dubins' car" is related to the paper by L. E. Dubins. In this paper, the theorem on the number and type of optimal control switches was proved for time-optimal problems with such dynamics. An identical description of dynamics was used by R. Isaacs and, more than one hundred years ago, by A. A. Markov.
The difference of the second model is in the presence of some additional control w. By means of it, we can change the magnitude of the linear velocity instantaneously. For w equal to one, the car moves forward, for w equal to minus one, it goes backwards. The time-optimal control problem for such a model was investigated in the paper by J. A. Reeds and L. A. Shepp.
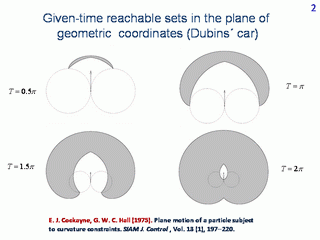
Let us fix the geometrical state and direction of the forward motion at the initial instant. For Dubins' car, the forward motion direction coincides with the velocity direction. On the slide, the form of reachable sets at given instants is shown. These are sets of points which are reachable from the initial state at a given time. We will call them the given-time reachable sets. The structure of the given-time reachable sets for Dubins' car is investigated in the paper by E. J. Cockayne and G. W. C. Hall.
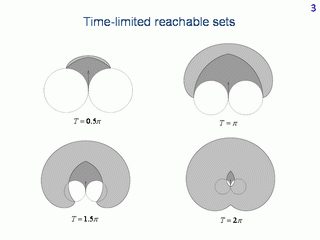
Similar reachable sets but by a given time are depicted. These are sets of points which are reachable from the initial state within a given time. We call them the time-limited reachable sets. More dark colouring is related to the parts which show the difference comparing to the given-time reachable sets.
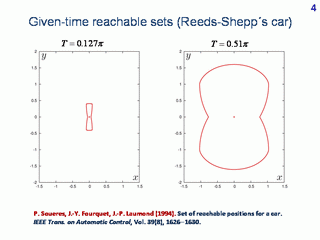
For Reeds-Shepp's car, given-time reachable sets are symmetrical with respect to both vertical and horizontal axes. Moreover, they grow monotonically with time, and, therefore, coincide with corresponding time-limited reachable sets. Due to these facts, Reeds-Shepp's model is so popular in papers on theoretical robotics. The structure of reachable sets for Reeds-Shepp's car was investigated in the paper by P. Soueres, J.-Y. Fourquet, J.-P. Laumond.

Let us introduce a parameter "a" which determines the lower bound on
the control w. If
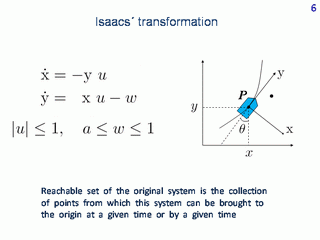
To construct numerically reachable sets in the plane of geometrical coordinates, let us apply Isaacs' transformation. We put the origin of the reference sytem at the position of object P. Let axis y be directed along the forward motion direction. Let us fix some point in the original plane. Then, in the reference coordinates, the motion of the point is described by the system to the left.
The time-limited or given-time reachable set in the plane of original coordinates coincides with the set of all reference points from which the origin of the reference system can be reached within a given or at a given time. The latter set will be called the solvability set.
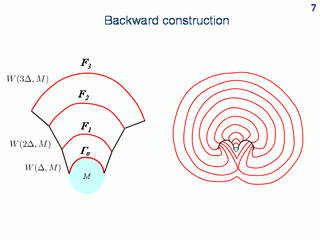
To construct given-time or time-limited solvability sets in the reference coordinates, we apply backward constructions. They are schematically shown here for the time-optimal problem. We move backwards in time with time step Δ. The target set not necessarily coincides with the origin and is not necessarily a single point. It can be any convex set in the plane.
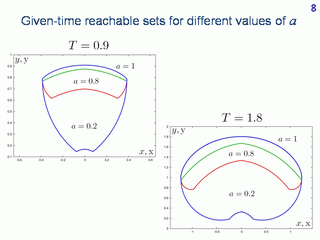
Here, the given-time reachable sets are shown for two instants. The computation is done for three values of parameter a. The target set in the backward computation is the origin of the reference system.
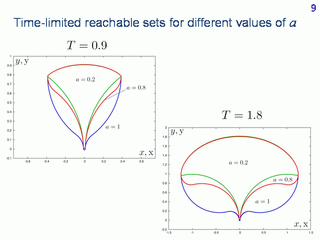
Here, similar pictures of the time-limited reachable sets are shown.
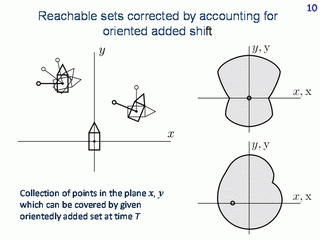
Let us fix a set shifted with respect to the origin and attach it rigidly to the car's body. We call it the oriented shift. Take this shifted set as a target for the reference system. The corresponding solvability set for such a target set consists of the reachable set constructed from zero in the plane of the original geometrical coordinates and corrected by accounting for the oriented added set rigidly attached to the car.
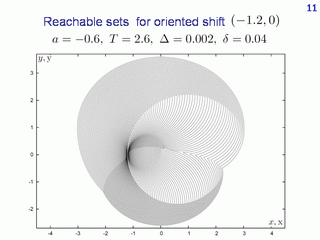
Here, we see a very small circle shifted horizontally to the left with respect to the origin. The given-time reachable sets corrected by accounting for the oriented added set are shown. In this case, the computed sets grow in all directions. Therefore they coincide with the corrected time-limited reachable sets. The value of the parameter a is -0.6.
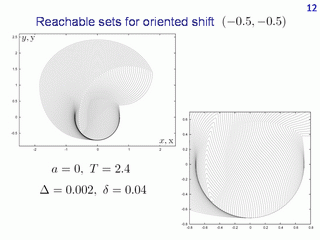
On this slide, some other oriented shift with respest to the origin is
considered. Parameter
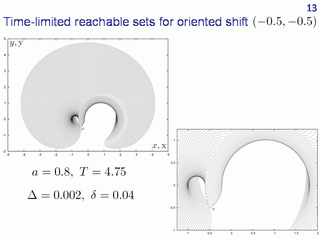
The same computation as in the previous slide but for the value of parameter a equal to 0.8 is shown. That is, we decrease the range of changing the possible linear velocity. The corrected time-limited reachable sets are depicted. In the case considered, they do not coincide with the corrected given-time reachable sets.
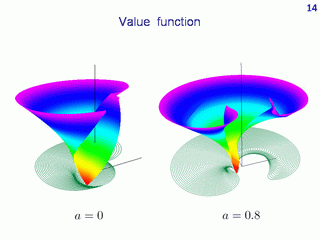
Here, graphs of the value function for two last examples are presented. In both examples, the value function is discontinuous.
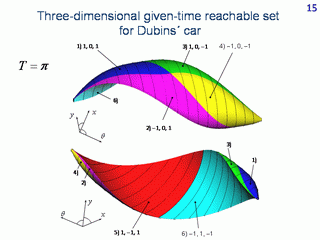
The reachable sets discussed before were reachable sets in the plane of the geometric coordinates of the car. Now, let us go to three-dimensional reachable sets. The third coordinate is the angle θ specifying the current direction of the velocity vector.
Three-dimensional reachable sets are only computed for Dubins' car, which means that the linear velocity magnitude is constant. The computation is performed for the given-time reachable sets only.
Two snapshorts correspoding to the instant π are presented. The colours mark the parts of the boundary with the same type of switching the control u. For example, the red surface is formed using controls of the type 1, -1, 1. (It is proved for Dubins' car that every boundary point of the reachable set can be reached using a piecewise constant control u with two switches at most.)
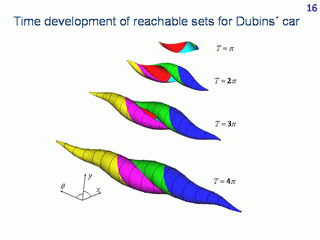
Here, the time development of the given-time reachable sets is shown. For small times, the reachable set is similar to a curved leaf. It becomes like a snail with increasing time.
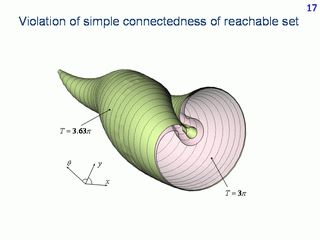
In this picture, the reachable sets for two instants are cut by the central plane which is parallel to the plane of geometrical coordinates x,y. The drawing shows the violation of simple connectedness of the three-dimensional reachable set.
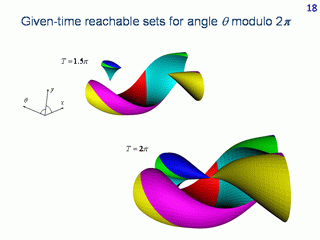
It is natural to consider the angle coordinate as being calculated modulo 2π. The sets obtained in this way are shown for the instants 1.5π and 2π.
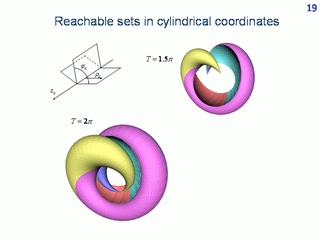
If one uses cylindrical coordinates instead of Cartesian ones, the following reachable sets are obtained.

Several related works by the authors are presented.