Download full text of the report (PDF format, 2363 KB)


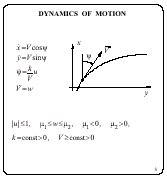
A model problem of aircraft tracking is
considered. Aircraft motion is described in the horizontal plane
x, y by a system of differential equations of the fourth
order. Here, x, y are geometrical coordinates of the
aircraft position; ![]() is
the heading; V is the velocity value; the constant k
is the maximal value of the lateral acceleration; u, w
are unknown controls, which obey geometric constraints.
is
the heading; V is the velocity value; the constant k
is the maximal value of the lateral acceleration; u, w
are unknown controls, which obey geometric constraints.
In general, a relation, that determines the
velocity dynamics, can be more complicated than the fourth
equation of the system. Such a relation can depend on many
parameters and can not be known exactly. Refusing a complicated
description, we use the equation 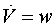 and interpret parameters
and interpret parameters 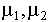 as constraints on possible values of the
longitudinal acceleration
as constraints on possible values of the
longitudinal acceleration
![]() .
.
The system is often used for description of motion of an aircraft, a car, and other objects with similar dynamics.
Current information about aircraft motion is represented in a
form of measurements of its position in the plane at discrete
time instants. The geometric constraint on the measurement error
is given. The heading ![]() and velocity V are not measured. An approach
based on a construction of the informational sets is applied for
solving the problem of aircraft tracking.
and velocity V are not measured. An approach
based on a construction of the informational sets is applied for
solving the problem of aircraft tracking.

As an informational set we mean a totality of all phase states of the system consistent with all measurements received up to the current instant.
Theoretical questions joined with informational sets in different problems were investigated in works of N.N.Krasovskii, A.B.Kurzhanskii, A.I.Subbotin, F.L.Chernous'ko and their colleagues. But a few works concern a construction of the informational sets in concrete problems. It is stipulated by the fact that in concrete cases the informational sets can have very complicated structure.
In the problem considered, the informational sets are built in a four-dimensional space and are not convex. More than that, they can be disconnected.
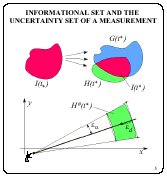
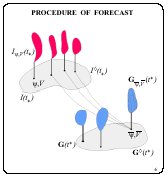
Explain now the general scheme of construction of the
informational sets. Let an informational set
![]() be constructed for the instant
be constructed for the instant
![]() ,
and suppose that the next measurement comes at the instant
,
and suppose that the next measurement comes at the instant
![]() .
Using the dynamics description, the forecast set
.
Using the dynamics description, the forecast set
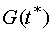 is built.
This is an attainability set of the controlled system at the instant
is built.
This is an attainability set of the controlled system at the instant
![]() with the set
with the set
![]() as the initial one. The uncertainty set
as the initial one. The uncertainty set
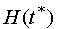 is put in correspondence to the measurement obtained at the instant
is put in correspondence to the measurement obtained at the instant
![]() .
This is a totality of all phase states
consistent with the measurement and the given constraints on the
measurement error. The informational set
.
This is a totality of all phase states
consistent with the measurement and the given constraints on the
measurement error. The informational set
![]() is constructed as the intersection of the sets
is constructed as the intersection of the sets
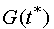 and
and
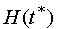 .
In the problem discussed, measurements of an aircraft position in
the horizontal plane are obtained, for example, from a radar.
The measurement error is
stipulated by errors in the direction and distance, and the
corresponding set
.
In the problem discussed, measurements of an aircraft position in
the horizontal plane are obtained, for example, from a radar.
The measurement error is
stipulated by errors in the direction and distance, and the
corresponding set
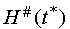 of positions in the horizontal plane appears. The set
of positions in the horizontal plane appears. The set
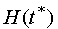 ,
being a set in the four-dimensional phase space, is cylindrical in coordinates
,
being a set in the four-dimensional phase space, is cylindrical in coordinates
![]() ,
V and has the set
,
V and has the set
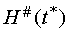 as a projection in the plane x, y.
Further, the sets
as a projection in the plane x, y.
Further, the sets
![]() are supposed to be convex.
are supposed to be convex.
Note two special properties of the equation system: 1) the third and fourth equations do not depend on the first and second ones, 2) the phase variables x, y are not present in the right-hand side of the first and second equations.
It allows to construct the informational sets in the
following
way. A projection 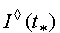 of
the informational set
of
the informational set ![]() into the plane
into the plane ![]() ,
V is considered. A set
,
V is considered. A set 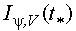 is put in correspondence to each point of the
set
is put in correspondence to each point of the
set 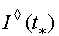 . Each set
. Each set 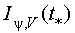 is a section of the set
is a section of the set ![]() by a plane {
by a plane {![]() =const, V=const} and
is described by its projection into the plane x, y. As the
first operation when building the full forecast set, we compute
the forecast set
=const, V=const} and
is described by its projection into the plane x, y. As the
first operation when building the full forecast set, we compute
the forecast set ![]() taking
the set
taking
the set ![]() as the initial
set.
as the initial
set.
Several motions from the set ![]() come to each point
come to each point ![]() ,
, ![]() of the set
of the set
![]() . Along each motion the
corresponding set
. Along each motion the
corresponding set ![]() is
transferred, and the transferred sets are further united. In such
a way, we obtain the set
is
transferred, and the transferred sets are further united. In such
a way, we obtain the set ![]() . Having implemented this operation for all pairs
. Having implemented this operation for all pairs ![]() ,
, ![]() , we obtain the forecast set
, we obtain the forecast set ![]() , which is represented in
the same form as the set
, which is represented in
the same form as the set ![]() .
.
The main difficulty is in the fact that the sets ![]() are not convex. We
consciously make some roughening when substitute the set
are not convex. We
consciously make some roughening when substitute the set ![]() by its convex envelope
by its convex envelope ![]() .
.
So, instead of the true forecast set ![]() , we obtain its upper estimate
, we obtain its upper estimate ![]() represented by a nonconvex
set
represented by a nonconvex
set ![]() and a totality of
convex sets
and a totality of
convex sets ![]() .
.
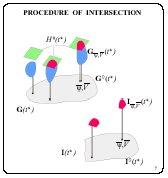
The informational set ![]() is an intersection of the forecast set
is an intersection of the forecast set ![]() and the uncertainty set
and the uncertainty set ![]() . The form of representation
of the set
. The form of representation
of the set ![]() and the
cylindrical property of the set
and the
cylindrical property of the set ![]() in the coordinates
in the coordinates ![]() ,
V permits us to implement this intersection in
a rather simple way. Namely, we intersect each set
,
V permits us to implement this intersection in
a rather simple way. Namely, we intersect each set ![]() with the set
with the set ![]() . These sets are convex and
lie in the plane x, y. Nonempty results of the
intersection compose the informational set
. These sets are convex and
lie in the plane x, y. Nonempty results of the
intersection compose the informational set ![]() .
.
Underline once more that under exact construction of the
informational sets their sections ![]() are not convex. In our constructions, the sets
are not convex. In our constructions, the sets ![]() are convex and give upper
approximations of the true sets
are convex and give upper
approximations of the true sets ![]() . We apply the operation of convexification from the
initial time instant t0.
. We apply the operation of convexification from the
initial time instant t0.
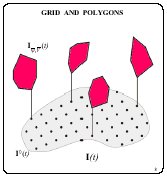
In practical building the informational sets, the set ![]() is given by a grid, and the
sets
is given by a grid, and the
sets ![]() , corresponding to
each node
, corresponding to
each node ![]() , V of
the grid, are convex polygons.
, V of
the grid, are convex polygons.
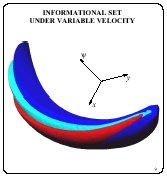
Choose in the set ![]() all nodes with the same value of the velocity V
and gather a totality of corresponding sets
all nodes with the same value of the velocity V
and gather a totality of corresponding sets ![]() . This totality represented
for different values of the coordinate
. This totality represented
for different values of the coordinate ![]() composes a three-dimensional set. If the grid
in
composes a three-dimensional set. If the grid
in ![]() is sufficiently
dense, then obtained informational set practically coincides with
the section of the set I(t)
for chosen value of V. The film shows three such
sets for three different values of V. Their "banana" form
is typical for the problem under discussion.
is sufficiently
dense, then obtained informational set practically coincides with
the section of the set I(t)
for chosen value of V. The film shows three such
sets for three different values of V. Their "banana" form
is typical for the problem under discussion.
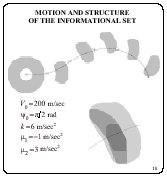
Elaborated program for the informational set construction
allows to implement calculations in a real-time tempo. The
simulation results are shown for the time interval 120 sec.
Projections of the informational set are shown in the plane x,
y. The initial uncertainty in ![]() was given from 0 to
was given from 0 to ![]() , and in V it was from 100 m/sec to 500
m/sec.
, and in V it was from 100 m/sec to 500
m/sec.
The large uncertainty in ![]() had stipulated the ring form of the forecast set in the
initial time interval. The thing solid line marks the trajectory
of the true motion. Measurements came with the time step of 20
sec.
had stipulated the ring form of the forecast set in the
initial time interval. The thing solid line marks the trajectory
of the true motion. Measurements came with the time step of 20
sec.
In intervals among the measurements appeared, the informational set grows; when the next measurement comes, the set fast decreases.
The informational set at the instant 53 sec is shown in
detail. Here, the whole projection is marked in light gray, the
layer corresponding to the velocity value of 277.8 m/sec is
shadowed in middle gray. Inside, one section of the informational
set is marked in dark gray for the value ![]() =1.173 rad. All these section gathered for all
admissible
=1.173 rad. All these section gathered for all
admissible ![]() compose the
layer (middle gray) for the given V.
compose the
layer (middle gray) for the given V.
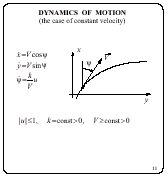
The case, when the velocity is known in advance and constant in time, is interesting itself. Here, the motion dynamics is described by a system of three differential equations. Respectively, the informational set is built in the three-dimensional space.
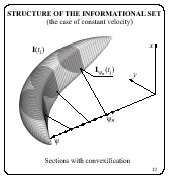
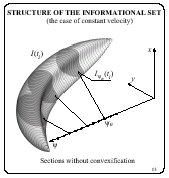
In the case when the velocity is known in advance and
constant
in time, the informational set is composed of the sections
(layers) which correspond to each node of the grid in ![]() . Each section is a convex
polygon because of the way of its building (Film 12). Without
convexification, the sections could be non-convex as presented in
the Film 13.
. Each section is a convex
polygon because of the way of its building (Film 12). Without
convexification, the sections could be non-convex as presented in
the Film 13.
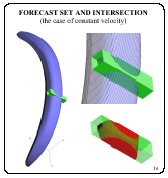
For some instant, the forecast set is shown in blue. The
uncertainty set of the measurement appeared colored in green. The
uncertainty set is cylindrical in the coordinate ![]() . The area of the
intersection and its result are shown in a large scale. The
obtained informational set is marked in red.
. The area of the
intersection and its result are shown in a large scale. The
obtained informational set is marked in red.
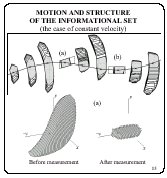
A fragment of the informational set motion in the interval of
32 sec is shown in a projection in the plane x, y. In this
interval, there are two measurements with the uncertainty sets in
the form of a parallelogram (a) and a rectangle (b). The crosses
mark positions of the true point. In the informational set, the
layers are shadowed which located in ![]() mostly close to its corresponding true
values.
mostly close to its corresponding true
values.
The three-dimensional structures are shown around the instant
(a): before (the forecast set) and after (the informational set
itself) taking into account the measurement at this instant. It
is seen that the informational set is evidently improved in the
non-observable coordinate ![]() :
the layers corresponding to non-admissible values of
:
the layers corresponding to non-admissible values of
![]() are eliminated - they
give empty intersections with the uncertainty set of the
measurement.
are eliminated - they
give empty intersections with the uncertainty set of the
measurement.
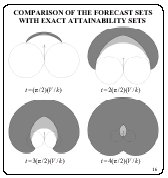
Remind, that the applied procedure of convexification leads
to
an error in the construction of the informational set. To
estimate this error, we compare the constructed forecast sets
with exact attainability sets calculated under special
conditions. Suppose that the initial position of an aircraft and
the initial heading are exactly known, and the value of the
velocity is also known and constant. For this case, the exact
formulae are known, which describe the frontier of the
attainability set in the projection in the plane x, y. The
comparison is illustrated by the attainability sets (contoured by
the solid line) for four time instants. The instants correspond
to change of the heading in ![]() . The forecast sets calculated by our algorithms are
shadowed in gray. The arrows mark the initial heading of the
velocity vector, and the circles represent trajectories with the
extreme controls u=-1 and u=1. Each figure has its
own scale. It is seen that the outer frontiers of the forecast
sets and the attainability sets practically coincide, but their
inner frontiers are different. (For calculation of the exact
attainability sets, the formulae were used from the works of
Yu.I.Berdyshev.)
. The forecast sets calculated by our algorithms are
shadowed in gray. The arrows mark the initial heading of the
velocity vector, and the circles represent trajectories with the
extreme controls u=-1 and u=1. Each figure has its
own scale. It is seen that the outer frontiers of the forecast
sets and the attainability sets practically coincide, but their
inner frontiers are different. (For calculation of the exact
attainability sets, the formulae were used from the works of
Yu.I.Berdyshev.)
Underline that the frontier of the exact attainability set can be calculated only for a point-wise initial set. But usually, in problems with incomplete information, it is necessary to build the forecast set having the initial set of a rather arbitrary form. Moreover, the construction has to be implemented in a three-dimensional space if the value of the velocity is known, and in a four-dimensional space if this value is unknown. The approach elaborated for building the forecast set does not give the exact result, but provides an upper approximation of the true sets and is rather simple in numerical realization.

The work was supported by the RFBR Grant N 00-01-00348