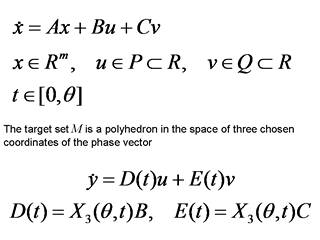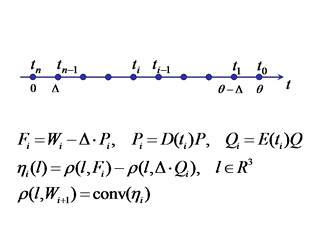English version

А.Г.Иванов, А.В.Ушаков

Адаптивное управление в трехмерных линейных системах с неизвестным уровнем динамической помехи

Game Theory and Management
Second International Conference on Game Theory and Management

Загрузить все слайды доклада с комментариями (формат PDF, 3389 KB)

Слайд 1

В первой части презентации рассматривается построение максимальных стабильных мостов для трехмерной (по целевому множеству) линейной дифференциальной игры. Во второй части разработанная процедура применяется для построения адаптивного управления в задачах, где априори не оговорено геометрическое ограничение на управление второго игрока.

Слайд 2

Построение максимальных стабильных мостов

Дифференциальная игра в исходном пространстве и эквивалентная игра

Слайд 3

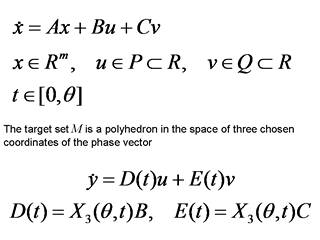
В исходной игре фазовый вектор может иметь любую размерность m ≥ 3, но выпуклое целевое множество зависит только от трех выделенных компонент фазового вектора. Стандартной заменой переменных переходим к эквивалентной дифференциальной игре третьего порядка без фазовой переменной в правой части. Предполагаем, что ограничения P, Q на управления первого и второго игроков — отрезки.

Аппроксимирующая игра

Слайд 4

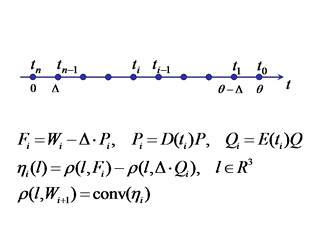
Для построения максимального стабильного моста в рамках аппроксимирующей игры разбиваем ось времени с шагом Δ влево от момента окончания θ точками t_i, при этом t₀=θ. На каждом шаге замораживаем динамику эквивалентной системы. Результатом построений будут t-сечения W_i=W(t_i) ⊂ R³ аппроксимирующего максимального стабильного моста W.

Построение сечений производится в попятной процедуре: на первом шаге на основе целевого выпуклого многогранника строится выпуклый многогранник W₁; на втором шаге на основе W₁ идет построение выпуклого многогранника W₂ и т.д.

Построение очередного сечения W_i+1 моста сводится к операциям над выпуклыми многогранниками, а именно, к построению алгебраической суммы F_i многогранника W_i и отрезка −Δ·P_i (учет действия первого игрока) и построению геометрической разности многогранника F_i и отрезка Δ·Q_i (учет действия второго игрока). Последнее эквивалентно взятию выпуклой оболочки разности ρ(·, F_i) − ρ(·, Δ·Q_i) опорных функций множеств F_i и Δ·Q_i.

Для непрерывной, положительно однородной, кусочно-линейной функции γ : l → γ(l) с выпуклыми конусами линейности используем следующее представление: вводим на единичной сфере S сетку (граф) G(γ), определяемую пересечением сферы с конусами линейности функции γ. В каждом узле G(γ) записываем значение функции γ.

При построении опорной функции ρ (·, W_i+1) многогранника W_i+1 требуем, чтобы все конусы линейности функции ρ(·, W_i) были трехгранными и, соответственно, секторы сетки G(ρ(·, W_i)) — треугольными. Для этого нужно разбить секторы начальной сетки на треугольные и в дальнейшем при образовании новых сеток вводить в случае необходимости дополнительное разбиение (триангуляцию сетки).

Учет действия первого игрока

Слайд 5

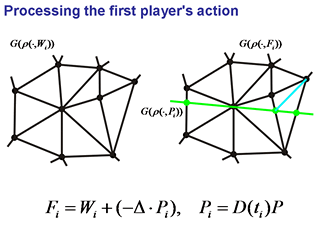
Сетка G(ρ(·, F_i)) есть результат наложения сеток G(ρ(·, W_i)) и G(ρ(·, P_i)). Поскольку P_i — отрезок в R³, то G(ρ(·, P_i)) представляет собой окружность на сфере S — пересечение сферы с проходящей через нуль плоскостью, ортогональной P_i. При наложении сеток появляются новые узлы. Поэтому при построении сетки G(ρ(·, F_i)) устанавливаем дополнительные связи для того, чтобы конусы линейности функции ρ(·, F_i) были трехгранными.

Учет действия второго игрока

Слайд 6

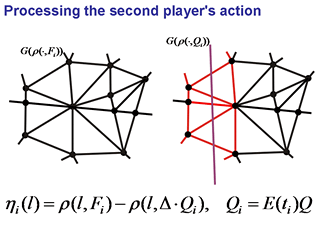
Пересчитываем значения опорной функции ρ(·, F_i) в узлах сетки G(ρ(·, F_i)) с учетом действия второго игрока. Получаем функцию η_i(·).

Для перехода к опорной функции многогранника W_i+1 в графе G(ρ(·, F_i)) следует отбросить узлы, связанные с "нарушением" выпуклости функции η_i(·).

Для проведения овыпукления разработана итерационная процедура. Организуем список "подозрительных" связей между узлами. Первоначально в этот список заносятся связи сетки G(ρ(·, F_i)), "разрубаемые" графом G(ρ(·, Q_i)) и соседние к ним. Затем идет корректировка этих связей, суть которой в исправлении нарушений локальной выпуклости. При этом список подозрительных связей может пополняться другими связями. Наоборот, связи, удовлетворяющие условиям локальной выпуклости, удаляются из списка. Процесс заканчивается при исчерпании массива подозрительных связей.

Базовые статьи

Слайд 7

При разработке алгоритма построения максимального стабильного моста использованы идеи из указанных на слайде статей.

Алгоритм построения максимального стабильного моста

Слайд 8

Здесь показана схема алгоритма построения моста. Она базируется на пошаговой процедуре построения сечений. Итерационная процедура овыпукления является наиболее затратной при вычислении очередного сечения.

Модельные примеры

Слайд 9

Приведенная на слайде динамика в случае k = 0 описывает материальную точку на прямой, в случае k = 1 — конфликтно-управляемый осциллятор. Управлением u распоряжается первый игрок, управлением v — второй.

Нахождение функции цены в двумерной игре (при помощи трехмерного моста)

Слайд 10

В двумерной игре с фиксированным моментом окончания терминальную функцию платы γ возьмем в виде γ(x) = max{|x₁|, |x₂|}. Нас интересует функция цены.

Для построения надграфика функции цены рассмотрим игру третьего порядка с целевым множеством M в виде срезки на некотором уровне c^* надграфика функции платы для двумерной игры. Тогда t-сечение моста трехмерной игры будет срезкой на уровне c^* надграфика функции цены двумерной игры для этого же момента t.

Целевое множество

Слайды 11, 12

Здесь показано целевое множество трехмерной игры: вид сбоку и вид снизу.

Сечения моста для разных моментов времени

Слайды 13–22

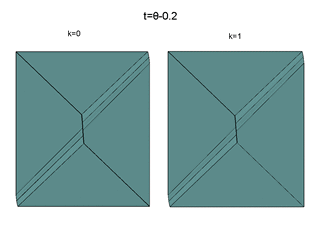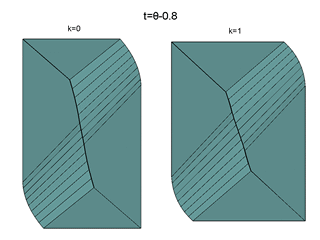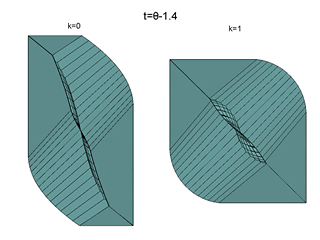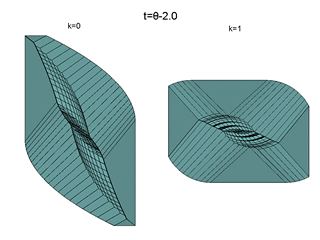
Изображены сечения моста исследуемых трехмерных игр для разных моментов времени.
Слева для материальной точки, справа — для маятника.
Представлен вид "снизу" — со стороны отрицательных значений оси c.

Слайд 23

Адаптивное управление

Адаптивное управление

Слайд 24

Рассматривается задача о построении адаптивного управления в линейных системах с неизвестным уровнем динамической помехи. Цель полезного управления — приведение n выделенных компонент фазового вектора на выпуклое, ограниченное целевое множество в фиксированный момент времени θ. Полезное управление стеснено геометрическим ограничением. Динамическая помеха (управление второго игрока) предполагается ограниченной, но уровень ограничения заранее неизвестен.

Принцип адаптивного управления

Слайд 25

На этом слайде пояснены требования к адаптивному управлению.

Семейство стабильных мостов для формирования адаптивного управления

Слайд 26

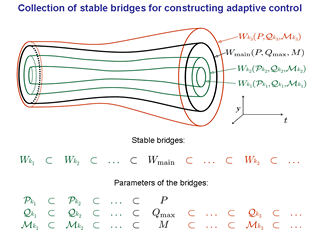
Рассматривается упорядоченное семейство стабильных мостов. Каждый мост определяется тройкой: ограничение на управление первого игрока, ограничение на управление второго игрока, целевое множество.

Главный мост W_main соответствует тройке P, Q_max, M, где множества P и M заданы по постановке задачи, а множество Q_max трактуется как геометрическое ограничение на помеху, которое первый игрок считает "разумным" в рассматриваемой задаче. Предполагаем, что каждое из множеств P, Q_max, M содержит нуль своего пространства.

В случае n = 2 алгоритмы построения адаптивного управления реализованы ранее. Рисунок вложенной системы мостов приведен именно для двумерного случая.

В данной работе рассматривается случай трехмерного целевого множества. Следовательно, t-сечения мостов также являются трехмерными. Для построения мостов используется алгоритм, описанный в первой части презентации.

Моделирование адаптивного управления

Слайды 27–43

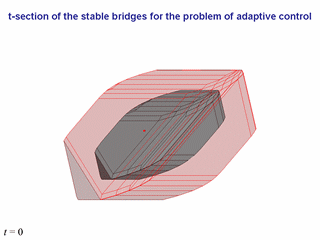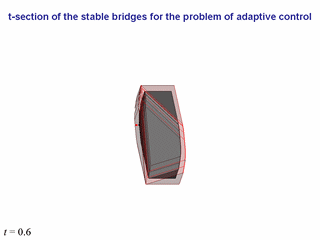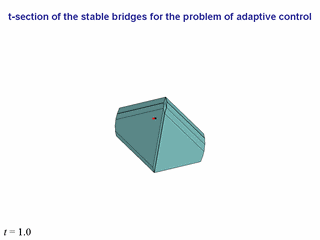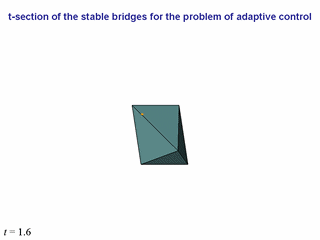
Представим результаты моделирования для некоторой системы (ее не выписываем). За первого игрока используется адаптивное управление, за второго — случайная помеха. Для построения адаптивного управления применяем известный в теории дифференциальных игр принцип экстремального прицеливания.

На идущей далее последовательности слайдов показано поведение фазового состояния системы относительно t-сечений главного моста.

На начальном промежутке времени фазовая точка находится вне главного моста (точка красного цвета). Поэтому для построения адаптивного управления используются t-сечения внешних мостов. Розовым цветом показано то из них, на которое производится прицеливание при построениии управления. В некоторый момент времени фазовая точка попадает внутрь главного моста (внутри главного моста она изображается оранжевым цветом). В таких ситуациях изображаются только t-сечения главного моста, хотя управление осуществляется прицеливания на t-сечение некоторого моста, вложенного в главный. Сечения вложенных мостов рассчитываются очень просто: умножением соответствующего t-сечения главного моста на коэффициент k < 1.

В левом нижнем углу указан момент текущего времени. Соседние слайды с одинаковым моментом времени различаются точкой зрения. При переходе от одного момента времени к другому ракурс не меняется.

Страница сектора Пацко