

''Homicidal chauffeur'' game was introduced and described by Rufus Isaacs in his report for the RAND Corporation in 1951. Here, the title page of this report and a figure illustrating the swerve maneuver are shown. A detailed description of the problem was given in the book ''Differential games'' published in 1965.
In this problem, a ''car'' whose radius of turn is bounded from below and the magnitude of the linear velocity is constant pursues a non-inertia ''pedestrian'' whose velocity does not exceed some given value.

On this slide, we see a description of the dynamics of players P and E. Here, xp and yp are the coordinates of the geometrical position, θ is the angle between the linear velocity vector and the vertical axis. Further, w is the magnitude of the linear velocity, R is the minimal radius of turn, u is the control constrained as |u| ≤ 1. For player Е, xe , ye are the geometric coordinates of the state, v is the control constrained as |v|≤ρ.
Normalizing the time and geometric coordinates, one can achieve w=1, R=1.
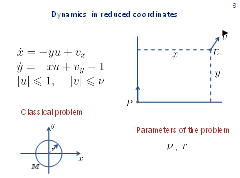
Put the origin of the reference system at the current position of player P and direct axis y along P's velocity vector. Then the current state of player E in the reference coordinates is described by the system of the second order. In the classical Isaacs' problem, the objective of player P is to bring the phase state to the target set M as soon as possible. Player E strives to prevent that. As the target set M, a circle of radius r centred at the origin is taken. So, we have two parameters of the game: ν and r. Admissible controls are feedback controls.
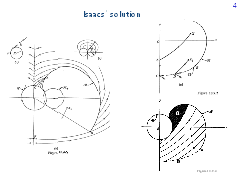
R. Isaacs investigated the problem for some parameter values using his method for solving differential games. The basis of the method is the backward computation of characteristics of an appropriate partial differential equation. First, some primary region is filled out with regular characteristics, then a secondary region is filled out, and so on. The final characteristics in the plane of the state variables coincide with optimal trajectories.
This slide shows figures from the book by R.Isaacs. The solution is symmetric with respect to the vertical axis. The upper part of the vertical axis is a singular line. Time-optimal trajectories meet this line at some angle and then go along it towards the target set M. According to Isaacs' terminology, the line is called universal. The part of the vertical axis adjoining the target set from below is also a universal singular line. Optimal trajectories go down along it. The rest of the vertical axis is a dispersal singular line: two optimal paths emanate from every point of it. On the barrier line B the value function is discontinuous. The side of the barrier line where the value of the game is smaller will be called positive. The opposite side is negative.
The equivocal singular line emanates tangentially from the terminal point of the barrier. It separates two regular regions. Optimal trajectories that come to the equivocal curve split into two paths: the first one goes along the curve, and the second one leaves it and comes to the regular region on the right.
The equivocal curve is described through an ordinary differential equation which is not integrated explicitly. Therefore, there is no any explicit description of the value function in the region between the equivocal and barrier lines. The most difficult for the qualitative investigation is the ''rear'' shaded part denoted by R.Isaacs with a question. He could not obtain a solution for this region.
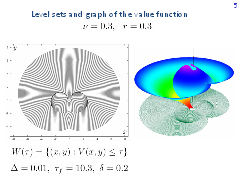
Our presentation will be accompanied by results of the numerical construction of level sets of the value function V(x, y). The computations are performed using our algorithm developed for time-optimal games in the plane. The lines on the boundary of the sets W(τ), τ > 0, consisting of points (x, y) where the equality V(x, y) = τ holds, will be called fronts (isochrones).
On the left picture, level sets of the value function computed until the time τf =10.3 are shown. The level sets are depicted with the time step δ=0.2. The parameter ν is equal to 0.3, the parameter r is 0.3. The graph of the value function is shown to the right. The value function is discontinuous on the barrier line and on a part of the boundary of the target set. In the case considered, the value function is smooth in the above mentioned rear domain.
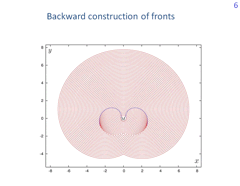
Let us explain briefly the backward procedure. We find a curve on the boundary of the target set, which Isaacs called usable part. Player P can guarantee the trajectory to be brought to the target set through this curve only. Take the usable part as zero front. Going back from this line with a given time step δ, we construct the front corresponding to the time τ = δ. Then compute the front corresponding to the time 2δ, and so on. Level set of the value function corresponding to the backward time τ is bounded by the front at this time, the adjoint barrier lines, and some curves on the boundary of the target set.

John Breakwell and Antony Merz continued the investigation of the homicidal chauffeur game in Isaacs' setting. Unfortunately, only two very short papers were published. On the left, we see the title page of the PhD-thesis made by A. Merz under supervision of J.Breakwell at the Stanford University. The complete solution is described in this thesis.
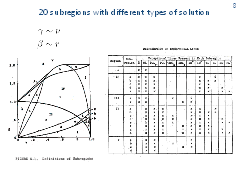
This slide presents a picture and a table from the thesis. They show the partition of two-dimensional parameter space into 20 subregions. A. Merz used symbols γ, β for the notation of parameters.
A.Merz investigated the qualitative structure of optimal trajectories and the type of singular lines for every subregion. All types of singular curves (dispersal, universal, equivocal, and switch lines) described by R. Isaacs for differential games in the plane appear in the homicidal chauffeur game. In the thesis, A.Merz suggested to distinct some subtypes of singular lines and consider them separately. For example, he introduced the notion of focal singular lines which are universal ones but with tangential approach of optimal trajectories.
The thesis contains many pictures explaining the type of singular lines and the structure of optimal trajectories. By studying them, one can easily realise how the solution depends on the parameters.
The work performed by A. Merz seems to be fantastic, and his thesis, to our opinion, is the best research among those devoted to concrete model problems.
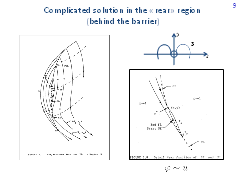
The figure to the left shows the structure of optimal trajectories in that part of the plane that adjoins the negative side of the barrier. The parameters correspond to subregion IIe. That is, we see a rear part denoted by R. Isaacs with a question sign. For subregion IIe, very complicated situation takes place.
Symbol PDL denotes the dispersal line controlled by player P. Two optimal trajectories emanate from every point of this line. Player P controls the choice of the side to which trajectories come down.
Figure to the right shows details of the behavior of optimal trajectories near switch envelope (SE) and focal line (FL). A. Merz as well as R. Isaacs used the symbol φ for the notation of the control of player P. In the presentation, the corresponding notation is u. Singular curve SE is specified as follows. Optimal trajectories approach it tangentially. Then one trajectory goes along this curve, and the other (equivalent one) leaves it at some angle. Therefore, line SE is similar to an equivocal singular line. The thesis contains arguments according to which switch envelope should be better considered as an individual type of singular line.
The dotted curves on the left figure mark boundaries of level sets (in other words, isochrones or fronts) of the value function.
The value function is not differentiable on the line composed of the curves PDL, SE, FL, and SE.
We undertook many efforts to compute value function for parameters from subregion IIe. But it was not succeeded, since we could not obtain corner points that must present on fronts to the negative side of the barrier. One of possible explanations to this failure can be the following. The subregion IIe is very small, and the effect is so subtle that it can not be detected even for very fine discretizations.
We think that the computation of level sets of the value function for the parameter subregions where the solution structure changes very rapidly, dependent on the parameters, can be considered as a challenge for differential game numerical methods being presently developed by different scientific teams.
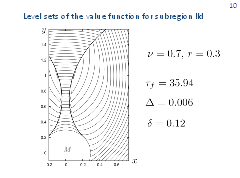
The figure shows our computation results for the case where fronts have corner points in the rear domain. However, the values of parameters correspond not to subregion IIe but to subregion IId. In this case, switch envelope curve SE remains but focal line FL disappears.
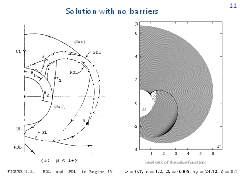
For some subregions of parameters, barrier lines on which the value function is discontinuous disappear. A. Merz described a very interesting transformation of the barrier line into two close to each other dispersal curves of players P and E.
Figure to the left presents a picture from the thesis by A. Merz that corresponds to subregion IVc. Numerically constructed level sets of the value function are shown in the figure to the right. When examining it, it might seem that some barrier line exists. But this is not true. We have exactly the case like the one shown in the figure to the left. An enlarged fragment of the figure is given on the next slide.
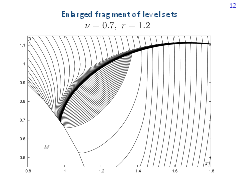
The curve composed of fronts' corner points above the accumulation region is the dispersal line of player E. The curve composed of corner points below the accumulation region is the dispersal line of player P. The value function is continuous in the accumulation region. To see where (in the considered part of the plane) the point of a maximal value of the game is located, additional fronts are shown. The point of the maximal value has the coordinates x =1.1, y = 0.92. The value function at this point is equal to 24.22.
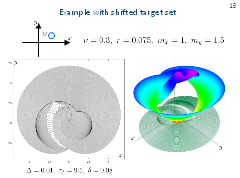
In the classical homicidal chauffeur setting, the target set is a circle centered at the origin. If the center of the target circle is shifted from y -axis, the symmetry of the solution with respect to y -axis is destroyed. The arising front structure to the negative side of barrier lines can be very complicated. One of such examples computed by the authors is presented here. The picture to the left gives level sets of the value function, the one to the right presents the graph of the value function. The target circle of radius 0.075 is centred at the point with the coordinates mx =1, my =1.5. The computation time step Δ is 0.01. The point of a maximal value of the game lies in the second quadrant. The value function at this point is equal to 9.5. The fronts are depicted with the time step δ=0.08.
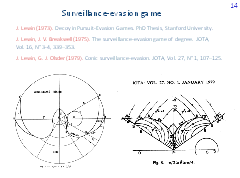
In the PhD thesis by Josef Lewin performed as well under supervision of J. Breakwell, in the joint paper by J. Breakwell and J. Lewin, and also in the paper by J. Lewin and Geert Jan Olsder, both dynamics and constraints on the controls of the players are practically the same as in Isaacs' setting but the objectives of the players differ. Namely, player E tries to bring the state vector to the target set M as soon as possible, whereas player P strives to prevent that. In the first and second works, the target set is the complement of an open circle centered at the origin. The left picture is from Lewin's PhD-thesis. In the third publication, the target set is the complement of an open cone with the apex at the origin. The right picture is taken from the paper by Lewin and Olsder.
The practical aspect related to the original context concerning two moving vehicles is the following: player E tries, as soon as possible, to escape from some detection zone attached to the geometric position of player P, whereas player P strives to keep his opponent in the detection zone as long as possible. Such a problem was called a surveillance-evasion game. To solve it, J. Breakwell, J. Lewin, and G. Olsder applied Isaacs' method.
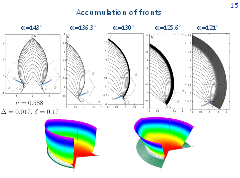
In the surveillance-evasion game with the conic target set, examples of transition from finite values of the game to infinite values are of interest and can be easily constructed.
The upper pictures show level sets of the value function for five values of parameter α which specifies the semi-angle of the nonconvex conic detection zone. Since the solution to the problem is symmetric with respect to y-axis, only the right half plane is shown for four of five figures. The pictures are ordered from greater to smaller α.
In the first picture, the value function is finite in the set that adjoins the target cone and is bounded by the curve a'b'cba. In the third picture, a situation of the accumulation of fronts is presented. Here, the value function is infinite on the line fe and finite on the arc ea. The value function has a finite discontinuity on the arc be. The graph of the value function corresponding to the third picture is shown in the lower left figure.
The second picture in the upper row shows a transition case from the first to the third picture.
In the fifth picture, the fronts propagate slowly to the right and fill out (outside the target set) the right half-plane as the backward time τ goes to infinity. The lower right figure gives a graph of the value function for this case.
The fourth picture in the upper row shows a transition case between the third and fifth pictures.
Let us return to problems where player P minimizes and player E maximizes the time of reaching the target set M.
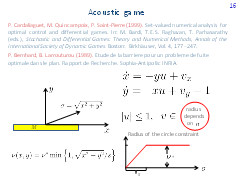
Pierre Cardaliaguet, Marc Quincampoix, and Patrick Saint-Pierre have considered an ''acoustic'' variant of the homicidal chauffeur problem suggested by Pierre Bernhard.
It is supposed that the constraint ν on the control of player E depends on the state (x, y). Namely, the constraint is constant and equal to ν*, if the distance σ to the origin is greater than a given value s. If the distance to the origin is less than s, the dependence is linear.
The applied aspect of the acoustic game: object E should not be very loud if the distance between him and object P is small.
P. Cardaliaguet, M. Quincampoix, and P. Saint-Pierre investigated the acoustic problem using their own method for numerical solving differential games which goes back to the viability theory. It was established that one can choose the values of parameters in such a way that the set of states where the value function is finite will contain a hole in which points the value function is infinite. Especially easy such a hole can be obtained if the target set is a rectangle stretched along the horizontal axis.
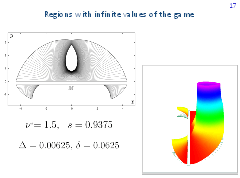
These figures demonstrate an example of the acoustic problem with the hole. The level sets of the value function and the graph of the value function are shown. The value of the game is infinite outside the set filled out with the fronts. An exact theoretical description of the arising hole and the computation (both analytical and numerical) of the value function near the boundary of the hole seems to be very complicated problem.

The model of the dynamics of player P in Isaacs' setting is the simplest one among those used in mathematical publications for the description of the car motion (or the aircraft motion in the horizontal plane). In this model, the trajectories are curves of bounded curvature. In the paper by Andrey A. Markov published in 1889, four problems related to the optimization over the curves with bounded curvature have been considered. The first problem can be interpreted as a time-optimal control problem where a car has the dynamics of player P. Similar interpretation can be also given to the main theorem of the paper by Lester E. Dubins published in 1957. The word ''car'' is not used neither in the paper by A. Markov, nor in the paper by L. Dubins. In Markov's paper, problems of railway construction are mentioned. In modern works on theoretical robotics, objects with the classical dynamics of player P are called ''Dubins' car''.
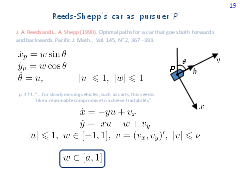
The next in complexity is the car model from the paper by James A. Reeds and Lawrence A. Shepp. The control u, as usual, determines the angular velocity of motion. An additional control w is responsible for the instantaneous change of the linear velocity magnitude. In particular, the car can instantaneously change the direction of motion to the opposite one.
A non-inertia change of the linear velocity magnitude is a mathematical idealization. But, citing Reeds and Shepp, ''for slowly moving vehicles, such as carts, this seems like a reasonable compromise to achieve tractability''.
Let us replace Dubins' car by Reeds-Shepp's car in the description of the homicidal chauffeur dynamics.
Player P is responsible for the controls u and w, player E steers with the control v.
It is natural to consider problems where the range for changing the control w is a segment [a, 1]. Here, a is the parameter of the problem. If a = 1, classical homicidal chauffeur game is obtained. For a = -1, we have homicidal chauffeur game with Reeds-Shepp's car.
The homicidal chauffeur game where player P controls a car which is able to change his linear velocity magnitude instantaneously was considered by the authors of this presentation. We investigated numerically the dependence of the solution on the parameter a.
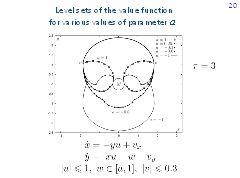
The figure presents the level sets of the value function, which correspond to one and the same time τ = 3 but to different values of the parameter a from -1 to 1. For all computations, the radius of the target set is r = 0.3 and the constraint on the control of player E is ν = 0.3. In case a = -1, player P controls Reeds-Shepp's car, and the obtained level set is symmetric with respect to both y-axis and x-axis. If a = 1, the level set for the classical homicidal chauffeur game is obtained.
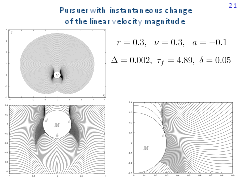
Here, families of level sets of the value function are shown for the following values of parameters of the problem: r = 0.3, ν = 0.3, a =-0.1. The time step Δ of the backward construction is 0.002 but the output step δ for fronts drawing is 25 greater.
The upper left figure shows the level sets of the value function computed backward in time till τf = 4.89. Precisely this value of the game corresponds to the last outer front and to the last inner front adjoining to the lower part of the boundary of the target circle M. The front structure is well seen in the enlarged fragment (lower left picture). Additionally, one more enlarged fragment is given to the right, which enables to examine the ends of the fronts running along the boundary of the set M from above to below. One can see a nontrivial character of changing the fronts near the lower border of the accumulation domain. The value function is discontinuous on the arc dhc. It is also discontinuous outside M on two short barrier lines emanating tangentially from the boundary of M. The right barrier is denoted by ce.
When solving time-optimal differential games of the homicidal chauffeur type with discontinuous value function, the most difficult question is the construction of optimal (or ε-optimal) strategies of the players. Let us demonstrate such a construction for this example.
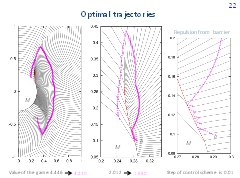
Let us present simulation results for ε-optimal strategies. The ε-optimal strategies are constructed based on the extremal aiming procedure developed by N. N. Krasovskii and A. I. Subbotin. The strategy of player P (E) is defined using the extremal shift to the nearest point (extremal repulsion from the nearest point) of the corresponding front. If the trajectory enters a prescribed layer attached to the positive (negative) side of the discontinuity line of the value function, then a control of player P (player E) pushes away from the discontinuity line is utilized on the next step of the control scheme.
Let us choose two initial points a = (0.3, -0.4) and b = (0.29, 0.1). The first point is located in the right half-plane below the front accumulation region, the second one is close to the barrier line on its negative side. The values of the game in the points a and b are V(a) = 4.446 and V(b) = 2.012, respectively.
In figures, the trajectories for ε-optimal strategies of the players are shown. The time step of the control procedure is 0.01. We obtain that the time of reaching the target set M is equal to 4.230 for the point a and 1.860 for the point b. Figure to the right shows an enlarged fragment of the trajectory emanated from the initial point b. One can see a sliding mode along the negative side of the barrier.
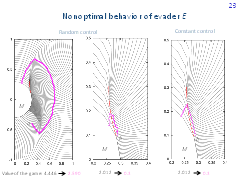
These pictures present trajectories for non-optimal behavior of player E and optimal behavior of player P.
The control of player E is computed using a random number generator (random choice of vertices of the polygon approximating the circle constraint of player E). The reaching time is 2.590 for the point a and 0.300 for the point b. One can see how the second trajectory penetrates the barrier line. In this case, the value of the game calculated along the trajectory drops jump-wise.
The picture to the right shows the trajectory for a constant control of player E, which is equal to one of the apexes of the polygon approximating the circle constraint of player E. The time of reaching the terminal set is 0.3.
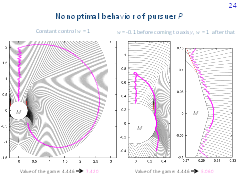
Here, simulation results for the optimal behavior of player E and nonoptimal behavior of player P are given. The picture to the left corresponds to the case where the control w of player P is constant and equal to 1. The time of reaching the target set is 7.42. The optimal time is 4.446. For the middle picture, the control w of player P is -0.1 until the trajectory comes to the vertical axis. After that, the control w equal to 1 is utilized. The right figure shows an enlarged fragment of the computations from the middle picture. The trajectory goes very close to the terminal set. The reaching time is 5.06.

Presently, numerical methods and algorithms for solving antagonistic differential games are intensively developed. Very often, the classical homicidal chauffeur game and its recent modifications are used as test or demonstration examples. Here, we see some of these papers. The attractiveness of the game is explained not only by its clear applied interpretation but also by the possibility of transition to the reference coordinates, which enables to deal with the two-dimensional state vector. Therefore, one can apply both general algorithms and algorithms that take into account the specifics of the plane.
Three persons whose contribution to the solution of the homicidal chauffeur problem is of great importance.

(March 2008)

(April 1987)

John Breakwell at a Stanford graduation

(about 1932-1936)

Rose and Rufus Isaacs with the daughter Ellen in Hartford, Connecticut before Isaacs went to Notre Dame University in about 1945.

Rose and Rufus Isaacs with their daughters Fran and Ellen on the shore of Lake Michigan in about 1947 at the time when Isaacs was at Notre Dame University.

Rufus Isaacs at his retirement party, 1979.

Everybody who read Isaacs' book knows these words: island, princess.

We are very grateful to Ellen S. Isaacs, John A. Breakwell, and Antony W. Merz for the photos.
A paper on this topic:
V.S.Patsko, V.L.Turova
Homicidal chauffeur game: history and modern studies. Scientific
report.
IMM Ural Branch of RAS. Ekaterinburg, Russia, 2008.
43 p.